Limit Cycle Oscillations

Limit Cycle Oscillations:

A limit cycle, sometimes referred to as a multiplier roundoff limit cycle, is a low-level oscillation that can exist in an otherwise stable filter as a result of the nonlinearity associated with rounding (or truncating) internal filter calculations. Limit cycles require recursion to exist and do not occur in nonrecursive FIR filters. As an example of a limit cycle, consider the second-order filter realized by

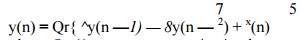
where Q_r {} represents quantization by rounding. This is stable filter with poles at 0.4375 ± j0.6585. Consider the implementation of this filter with 4-b (3- b and a sign bit) two’s complement fixed-point arithmetic, zero initial conditions (y(— 1) = y(—2) = 0), and an input sequence x(n) = |S(n), where S(n) is the unit impulse or unit sample. The following sequence is obtained;

Notice that while the input is zero except for the first sample, the output oscillates with amplitude 1/8 and period 6.

Limit cycles are primarily of concern in fixed-point recursive filters. As long as floating-point filters are realized as the parallel or cascade connection of first - and second-order subfilters, limit cycles will generally not be a problem since limit cycles are practically not observable in first- and second-order systems implemented with 32- b floating-point arithmetic [12]. It has been shown that such systems must have an extremely small margin of stability for limit cycles to exist at anything other than underflow levels, which are at an amplitude of less than 10^{— 3 8} . There are at least three ways of dealing with limit cycles when fixed-point arithmetic is used. One is to determine a bound on the maximum limit cycle amplitude, expressed as an integral number of quantization steps [13]. It is then possible to choose a word length that makes the limit cycle amplitude acceptably low. Alternately, limit cycles can be prevented by randomly rounding calculations up or down [14]. However, this approach is complicated to implement. The third approach is to properly choose the filter realization structure and then quantize the filter calculations using magnitude truncation [15,16]. This approach has the disadvantage of producing more roundoff noise than truncation or rounding [see (3.12)—(3.14)].