Laws of pendulum

Laws of pendulum

From the expression for the time period of oscilations of a pendulum the following laws are enunciated.

         ( i) The law of length

The period of a simple pendulum varies directly as the square root of the length of the pendulum. (i.e) T α l

(ii)The law of acceleration

The period of a simple pendulum varies inversely as the square root of the acceleration due to gravity.

(i.e) T α 1 g

(iii) The law of mass

 The time period of a simple pendulum is independent of the mass and material of the bob.

(iv)The law of amplitude

The period of a simple pendulum is independent of the amplitude provided the amplitude is small.

Note : The length of a seconds pendulum is 0.99 m whose period is two seconds.

2 = 2π.rt(l/g)

l=  9.81x 4 / 4 π²=0.99 m

Oscillations of simple pendulum can also be regarded as a case of angular SHM.

Let θ be the angular displacement of the bob B at an instant of time. The bob makes rotation about the horizontal line which is perpendicular to the plane of motion as shown in Fig..

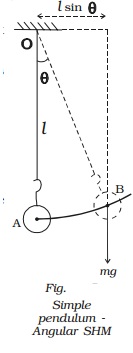
Restoring torque about O is τ = − mg l sin θ

τ = −m g l θ [ ∵ θ is sm all] ...(1)

Moment of inertia about the axis = m l ² ...(2)

If the amplitude is small, motion of the bob is angular simple harmonic. Therefore angular acceleration of the system about the axis of rotation is

α = r/l = -mgl θ / ml²

α = - (g/l) θ   ?.(3)

We know that α = −ω ² θ        ??.(4)

Comparing (3) and (4)

−ω ²θ = -(g/l) θ

angular frequency ω = rt(g/l)

Time period T = = 2π / ω = 2π .rt(l/g)

Frequency n = 1 / 2 π . rt(g/l)