Informed Search (Heuristic Search)

INFORMED SEARCH (HEURISTIC SEARCH)

Heuristic is a technique which makes our search algorithm more efficient. Some heuristics help to guide a search process without sacrificing any claim to completeness and some sacrificing it. Heuristic is a problem specific knowledge that decreases expected search efforts. It is a technique which sometimes works but not always. Heuristic search algorithm uses information about the problem to help directing the path through the search space. These searches uses some functions that estimate the cost from the current state to the goal presuming that such function is efficient. A heuristic function is a function that maps from problem state descriptions to measure of desirability usually represented as number. The purpose of heuristic function is to guide the search process in the most profitable directions by suggesting which path to follow first when more than is available.

Generally heuristic incorporates domain knowledge to improve efficiency over blind search. In AI heuristic has a general meaning and also a more specialized technical meaning. Generally a term heuristic is used for any advice that is effective but is not guaranteed to work in every case. For example in case of travelling sales man (TSP) problem we are using a heuristic to calculate the nearest neighbour. Heuristic is a method that provides a better guess about the correct choice to make at any junction that would be achieved by random guessing. This technique is useful in solving though problems which could not be solved in any other way. Solutions take an infinite time to compute.

Let us see some classifications of heuristic search.

Best First Search

Best first search is an instance of graph search algorithm in which a node is selected for expansion based o evaluation function f (n). Traditionally, the node which is the lowest evaluation is selected for the explanation because the evaluation measures distance to the goal. Best first search can be implemented within general search frame work via a priority queue, a data structure that will maintain the fringe in ascending order of f values. This search algorithm serves as combination of depth first and breadth first search algorithm. Best first search algorithm is often referred greedy algorithm this is because they quickly attack the most desirable path as soon as its heuristic weight becomes the most desirable.

Concept:

Step 1: Traverse the root node

Step 2: Traverse any neighbour of the root node, that is maintaining a least distance from the root node and insert them in ascending order into the queue.

Step 3: Traverse any neighbour of neighbour of the root node, that is maintaining a least distance from the root node and insert them in ascending order into the queue

Step 4: This process will continue until we are getting the goal node

Algorithm:

Step 1: Place the starting node or root node into the queue.

Step 2: If the queue is empty, then stop and return failure.

Step 3: If the first element of the queue is our goal node, then stop and return success.

Step 4: Else, remove the first element from the queue. Expand it and compute the estimated goal distance for each child. Place the children in the queue in ascending order to the goal distance.

Step 5: Go to step-3

Step 6: Exit.

Implementation:

Let us solve an example for implementing above BFS algorithm.

Figure

Step 1:

Consider the node A as our root node. So the first element of the queue is A whish is not our goal node, so remove it from the queue and find its neighbour that are to inserted in ascending order.

Advantage:

It is more efficient than that of BFS and DFS.

Time complexity of Best first search is much less than Breadth first search.

The Best first search allows us to switch between paths by gaining the benefits of both breadth first and depth first search. Because, depth first is good because a solution can be found without computing all nodes and Breadth first search is good because it does not get trapped in dead ends.

Disadvantages:

Sometimes, it covers more distance than our consideration.

Branch and Bound Search

Branch and Bound is an algorithmic technique which finds the optimal solution by keeping the best solution found so far. If partial solution can’t improve on the best it is abandoned, by this method the number of nodes which are explored can also be reduced. It also deals with the optimization problems over a search that can be presented as the leaves of the search tree. The usual technique for eliminating the sub trees from the search tree is called pruning. For Branch and Bound algorithm we will use stack data structure.

Concept:

Step 1: Traverse the root node.

Step 2: Traverse any neighbour of the root node that is maintaining least distance from the root node.

Step 3: Traverse any neighbour of the neighbour of the root node that is maintaining least distance from the root node.

Step 4: This process will continue until we are getting the goal node.

Algorithm:

Step 1: PUSH the root node into the stack.

Step 2: If stack is empty, then stop and return failure.

Step 3: If the top node of the stack is a goal node, then stop and return success.

Step 4: Else POP the node from the stack. Process it and find all its successors. Find out the path containing all its successors as well as predecessors and then PUSH the successors which are belonging to the minimum or shortest path.

Step 5: Go to step 5.

Step 6: Exit.

Implementation:

Let us take the following example for implementing the Branch and Bound algorithm.

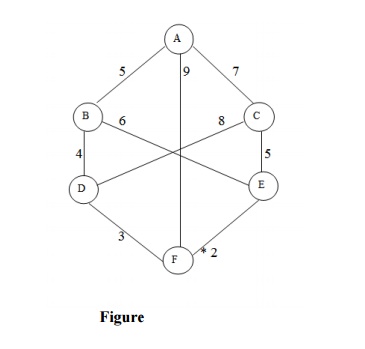
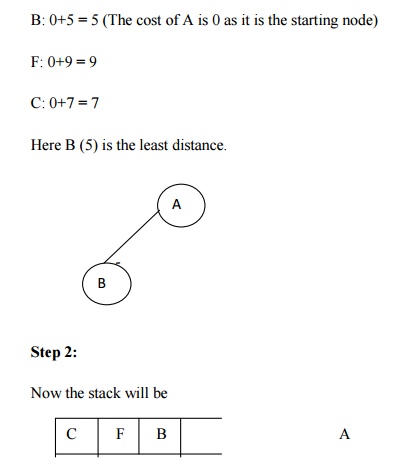
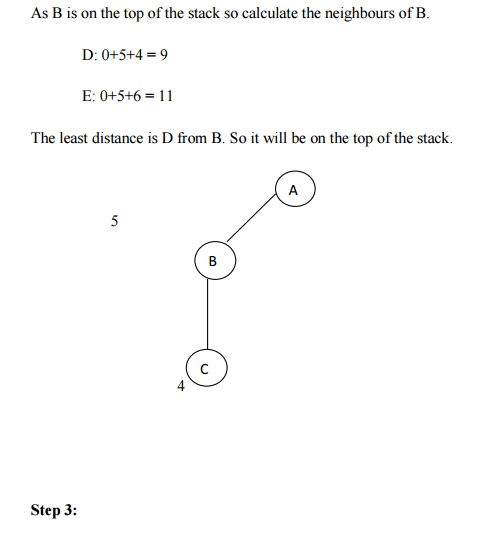
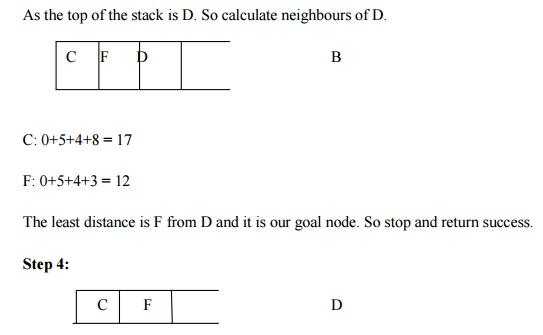
Hence the searching path will be A-B -D-F

Advantages:

As it finds the minimum path instead of finding the minimum successor so there should not be any repetition.

The time complexity is less compared to other algorithms.

Disadvantages:

The load balancing aspects for Branch and Bound algorithm make it parallelization difficult.

The Branch and Bound algorithm is limited to small size network. In the problem of large networks, where the solution search space grows exponentially with the scale of the network, the approach becomes relatively prohibitive.