Influence lines

INFLUENCE LINES

1 Influence lines

An influence line is a graph showing, for any given beam frame or truss, the variation of any force or displacement quantity (such as shear force, bending moment, tension, deflection) for all positions of a moving unit load as it crosses the structure from one end to the other.

Uses of influence line diagram

(i)                Influence lines are very useful in the quick determination of reactions, shear force, bending moment or similar functions at a given section under any given system of moving loads and

(ii)             Influence lines are useful in determining the load position to cause maximum value of a given function in a structure on which load positions can vary.

1.A simply supported beam of span 10m carries a udl of 20 kN/m over its central 4m length. With the help of influence line diagram, find the shear force at 3m from the left support.

2 Muller -Bresalu principle.

Muller -Bresalu principle states that, if we want to sketch the influence line for any force quantity (like thrust, shear, reaction, support moment or bending moment) in a structure,

(i)                we remove from the structure the restraint to that force quantity

(ii)             we apply on the remaining structure a unit displacement corresponding to that forces quantity.

For the two member determine bent in fig. sketch the influence line for V_A.

If we deftly apply Muller -Breslau to the problem, we can first remove support A and push A up by unit distance. Since the angle at B will remain unchanged, our unit displacement will result in a rigid body rotation of ?(=1/4 radian) about C. So the column CB will also have a horizontal displacement. (For the part AB, the diagram is just the influence line diagram for shear in a S.S beam)

The diagram for BC must be understood to be the influence of horizontal loads on the column on R_A.

principle on which indirect model analysis is based

The indirect model analysis is based on the Muller Bresalu principle.

Muller Breslau principle has lead to simple method of using models of structures to get the influence lines for force quantities like bending moments, support moments, reactions, internal shears, thrusts, etc.

To get the influence line for any force quantity (i) remove the restraint due to the force, (ii) apply a unit displacement in the direction of the force.

3.Begg'sformeterde

Begg'sdeformeter is a device to carry out indirect model analysis on structures. It has the facility to apply displacement corresponding to moment, shear or thrust at any desired point in the model. In addition, it provides facility to measure accurately the consequent displacements all over the model.

'dummy length'  modelsin tested with Begg'sformeterde.

Dummy length is the additional length (of about 10 to 12 mm) left at the extremities of the model to enable any desired connection to be made with the gauges.

Three types of connections possible with the model used with

Begg'sformeterde.

(i)                Hinged connection

(ii)             Fixed connection

(iii)           Floating connection

Use of a micrometer microscope in model analysis with Begg's deformeter

Micrometer microscope is an instrument used to measure the displacements of any point in the x and y directions of a model during tests with Begg'seformeterd.

Name the types of rolling loads for which the absolute maximum bending moment occurs at the mid span of a beam.

Types of rolling loads:

(i)                Single concentrated load

(ii)             Udl longer than the span

(iii)           Udl shorter than the span

Absolute maximum bending moment in a beam

When a given load system moves from one end to the other end of a girder, depending upon the position of the load, there will be a maximum bending moment for every section. The maximum of these maximum bending moments will usually occur near or at the mid span. This maximum of maximum bending moment is called the absolute maximum bending moment,

Mmaxmax.

The portal frame in fig. is hinged at D and is on rollers at A. Sketch the influence line for bending moment at B.

To get the influence line diagram for M_B, we shall introduce a hinge at B (and remove the resistance to bending moment). Now we get a unit rotation between BA and BC at B.

BC cannot rotate since column CD will prevent the rotation. BA would rotate freely (with zero moment). For ?=1 at B, displacement at A = 3m. The displaced position shows the influence line for M_B as shown in fig.

2.A  single  rolling  load  of  100  kN  moves  on  a  girder  of  span  20m.

(a) Construct the influence lines for (i) shear force and (ii) bending moment for a section 5m from the left support. (b) Construct the influence lines for points at which the maximum shears and maximum bending moment develop. Determine these values.

Solution:

To find maximum shear force and bending moment at 5m from the left support:

(i)  Maximum positive shear force

By inspection of the ILD for shear force, it is evident that maximum positive shear force occurs when the load is placed just to the right of D.

Maximum positive shear force = load * ordinate = 100 * 7.5

At D, SF_max + = 75 kN. (ii) Maximum negative shear force

Maximum negative shear force occurs when the load is placed just to

the left D.

Maximum negative shear force = load * ordinate = 100 * 0.25 At D, SF_max = -25 kN.

(iii) Maximum bending moment

Maximum bending moment occurs when the load is placed on the section D itself.

Maximum bending moment = load * ordinate = 100 * 3.75 = 375 kNm

(b)             Maximum positive shear force will occur at A. Maximum negative shear force will occur at B. Maximum bending moment will occur at mid span. The ILs are sketched in fig.

(i)                Positive shear force

Maximum positive shear force occurs when the load is placed at A. Maximum positive shear force = load * ordinate = 100*1

SF_maxmax + = 100 kN (ii) Negative shear force

Maximum negative shear force occurs when the load is placed at B. Maximum negative shear force = load * ordinate = 100 * (-1)

SF_maxmax = - 100 kN (iii) Maximum bending moment

Maximum bending moment occurs when the load is at mid span Maximum bending moment = load * ordinate = 100 * 5 = 500 kNm

3.Draw the ILD for shear force and bending moment for a section at 5m from the left hand support of a simply supported beam, 20m long. Hence, calculate the maximum bending moment and shear force at the section, due to a uniformly distributed rolling load of length 8m and intensity 10 kN/m run.(Apr/May 05)

Solution:

(a) Maximum bending moment:

Maximum bending moment at a D due to a udl shorter than the span occurs when the section divides the load in the same ratio as it divides the span.

(b) Maximum positive shear force

Maximum positive shear force occurs when the tail of the UDL is at D as it traverses from left to right.

(c) Maximum negative shear force

Maximum negative shear force occurs when the head of the UDL is at D as it traverses from left to right.

Maximum negative shear force = Intensity of load * Area of ILD under the load = 10(1/2*0.25*5)

Negative SF_max = 6.25 kN.

4.Two point loads of 100 kN and 200 kN spaced 3m apart cross a girder of span 15m  from  left  to  right  with   the  100  kN  load  loading.  Draw the influence line for shear force and bending moment and find the value of maximum shear force and bending moment at a section, 6m from the left hand support. Also, find the absolute maximum moment due to the given load system.

5.A train of 5 wheel loads crosses a simply supported beam of span 22.5 m. Using influence lines, calculate the maximum positive and negative shear forces at mid span and absolute maximum bending moment anywhere in the span.

Solution:

(a)             Maximum shear force

(i)                Positive shear force

To determine the load position to get the maximum positive shear force, let us keep all the loads to the right of C. Then move W₁ load to the left of 'C'by2.5 m. if the sign of shear increments S_i is negative, it will indicate that W₁ shall be retained at C

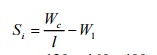
W = Total load on the span = 120 + 160 +400 + 260 +240 = 1182 kN.

C = Distance through which the load train is moved = 2.5 m

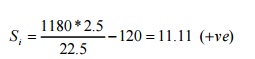
Since S_i is positive, the shear force increases due to thr shifting of W₁ to the left of C. Again, let us move W₂ to the left of C by 2.5 m to check whether the shera force further increases or not.

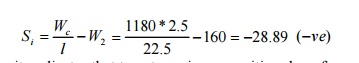
Since S_i is negative, it undicates that to get maximum positive shear force, W₂ should stay just right of C.

Maximum positive shear force = å(laodxordinate)

= 120 (-0.39) + 160 (0.5) +400 (0.39) +260(0.28) + 240 (0.17)

At C ,                SF_max + = 302.8 kN.

ii) Negative shear force

To determine the position of loads to get the maximum negative shear force, move the loads one by one to the right of C and computer the value of S_i.If S_i becomes negative it will indicate a decrease in negative shear force due to that movement.

First let us move the leading W₅ to the right of C by 2.5 m and calculate S_i

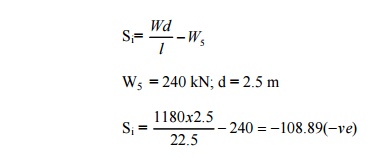
Since S_i is -ve it indicates that W₅ should stay just to the left of C.

Ordinates of ILD:

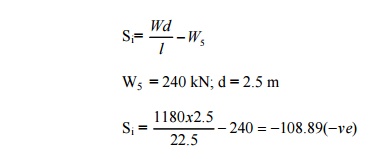
Maximum negative shear force at C = 240(-0.5)+260(-0.39)+(400(-0.278) +160(-0.167)

+120(-0.056)

F_max = 366.04 kN.

b)                Absolute maximum bending moment

i)                   Position of resultant of all loads

-

Taking moments about W₁, 120(0)+160(2.5)+400(5.0)+260(7.5)+240(10.0) =R. x

R = 1180kN

-

x                                                                                                                                    = 5,72m from W₁

ii)                                      Location of absolute maximum bending moment

Absolute maximum bending moment occurs under the load, which is nearest to the resultant (In'R'thisproblem. W₃ is nearest to the resultant 'R').The distance between C and R and the distance between C and W₃ shall be equal.

Distance between R and center of span(C) = ½ (0.72) =0.36 m

In this fig. Shows the IL for bending moment at the critical spot D, 10.89 m fro A.

Ordinates of ILD:

Maximum ordinate of ILD

Absolute maximum bending moment =120 (3.04)+160(4.33)+400(5.62)+260(4.41)+ 240 (3.2)

M_{max max} = 5220.2 kN.m

6) A girder a span of 18mis simply supported at the ends. It is traversed by a train of loads as shown in fig. The 50 kN load loading. Find the maximum bending moment which can occur (i) under the 200 kN load (ii) Under 50 kN load, using influence line diagrams.

Solution:

a)               Maximum bending moment

i)                       Under   200   kN

loads.

To get the maximum bending moment under W₃ the resultant R and W₃ should be at equal distances from the center of the span C.For that the point of action of resultant R should be determined first.

a)  Resultant of loads:

R = 450 kN

Taking  moments      about

^W4

200(3) +100 (3+2) +50(3 +2+3) = 450  x

-

x  = 3.33 from W₄

b)  Bending moment under 200 kN load

Distance between C and 200 kN load = Distance between C and R = 0.33/2 = 0.165 m.

Ordiantes of ILD :

=2.05 m

Bending moment under the 200 kN load

=                                                               200 (4.5) + 100 (2.97) + 100 (3.52) +50 (2.05) = 1651.5 kNm.

(ii)               Bending moment under the load 50 kN load

To get the maximum bending moment under W₁ , W₂ and R must be at equal distances from the centre of span ©. Distance between C and R = Distance between C and W₁ = ½ (2 -0.33 + 3) = ½ (4.67) = 2.335 m

Ordinates of ILD:

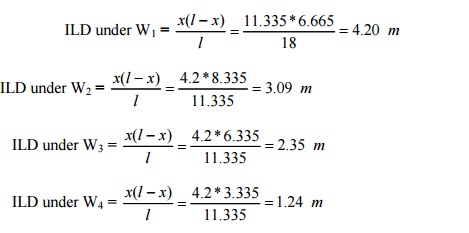
Bending moment under the load 50 kN load

= 4.2 (50) + 3.09 (100) +2.35 (200) +1.24 (100) = 1113 kN m.

6.Draw the I.L for reaction at B and for the support moment M_A at A for the propped cantilever in fig. Compute the I.L ordinates at 1.5 m intervals.

Solution:

Remove the restraint due to R_B (remove support B) Apply a unit displacement (upward).

When R_B = 1, then Y_XB is the displacement at section x due to unit load applied at B.

Fig. is the influence line diagram for R_B.

To get the I.L for M_A have to

(i)                      Introduce a hinge at A and

(ii)                   We have to apply a unit rotation at A. Instead we will apply a unit moment at A find the general displacement at any x from B. We will then divide the displacement by the actual rotation at A.

7.                             In a simply supported girder AB of span 2om, determine the maximum bending moment and maximum shear force at a section 5m from A, due to the passage of a uniformly distributed load of intensity 20 kN/m, longer than the span.

Solution:

(i) Maximum bending moment

Since the udl is longer than the , the criterion for maximum bending moment at a section is that the whole span should be loaded as shown in fig.

(ii) Maximum shear force

Maximum negative shear force at a section occurs when the head of the load reaches the section ((i.e. when the left portion AX is loaded and right portion XB is empty)

(iii)                 Maximum positive shear force:

Maximum positive shear force occurs at X when the tail of the load is at X as it moves from left to right. (i.e. AX is empty and the portion XB is loaded)

Maximum positive shear force = R_A