Chapter: Operations Research: An Introduction : Classical Optimization Theory
Inequality Constraints-Karush-Kuhn-Tucker (KKT) Conditions
Inequality Constraints-Karush-Kuhn-Tucker (KKT) Conditions
This section extends the Lagrangean method to problems with inequality constraints. The main contribution of the section is the development of the general Karush-Kuhn-Tucker (KKT) necessary conditions for determining the stationary points. These conditions are also sufficient under certain rules that will be stated later.
Consider the problem
Maximize z =f(X)
Subject to
g(X) ≤ 0
The inequality constraints may be converted into equations by using nonnegative slack variables. Let S2i ( ≥ 0) be the slack quantity added to the ith constraint gi(X) ≤ 0 and define
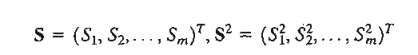
where m is the total number of inequality constraints. The Lagrangean function is thus given by
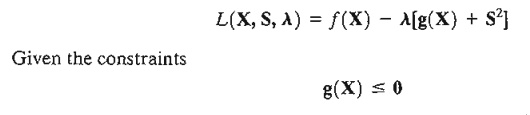
a necessary condition for optimality is that l be nonnegative (nonpositive) for maximization (minimization) problems. This result is justified by noting that the vector A measures the rate of variation of f with respect to g-that is,
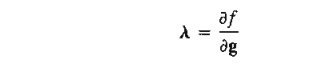
In the maximization case, as the right-hand side of the constraint g(X) ≤ 0 increases from 0 to the vector ¶g, the solution space becomes less constrained and hence f can-not decrease, meaning that l ≥ 0. Similarly for minimization, as the right-hand side of the constraints increases, f cannot increase, which implies that l≤ 0. If the constraints are equalities, that is, g(X) = 0, then A becomes unrestricted in sign (see Problem 2, Set 18.2d).
The restrictions on l holds as part of the KKT necessary conditions. The remaining conditions will now be developed.
Taking the partial derivatives of L with respect to X, S, and l, we obtain
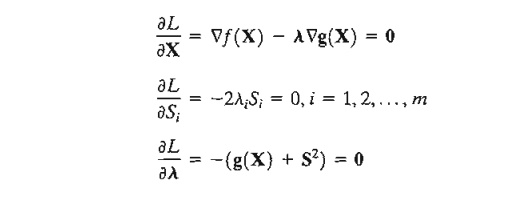
The second set of equations reveals the following results:
1. If li != 0, then Si2 = 0, which means that the corresponding resource is scarce, and, hence, it is consumed completely (equality constraint).
2. If Si2 > 0, then li = O. This means resource i is not scarce and, consequently, it has no affect on the value of t (i.e., li = ¶f/¶g = 0).
From the second and third sets of equations, we obtain
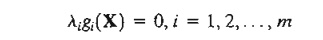
This new condition essentially repeats the foregoing argument, because if li > 0, gi(X) = 0 or Si2 = 0; and if gi(X) < 0, Si2 > 0, and li = 0.
The KKT necessary conditions for maximization problem are summarized as:
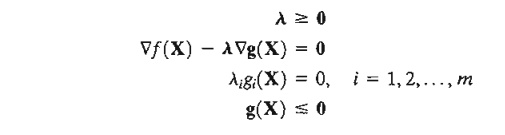
These conditions apply to the minimization case as well, except that l must be non-positive (verify!). In both maximization and minimization, the Lagrange multipliers corresponding to equality constraints are unrestricted in sign.
Sufficiency of the KKT Conditions. The Kuhn-Tucker necessary conditions are also sufficient if the objective function and the solution space satisfy specific conditions. These conditions are summarized in Table 18.1.
It is simpler to verify that a function is convex or concave than to prove that a solution space is a convex set. For this reason, we provide a list of conditions that are easier to apply in practice in the sense that the convexity of the solution space can be established by checking the convexity or concavity of the constraint functions. To pro-vide these conditions, we define the generalized nonlinear problems as
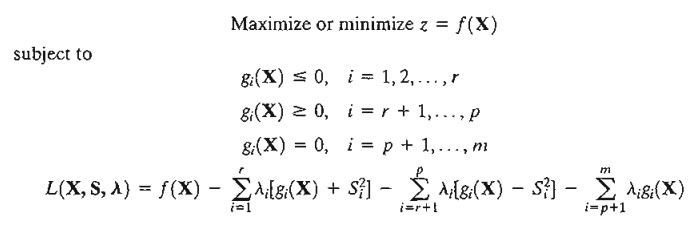
where li is the Lagrangean multiplier associated with constraint i. The conditions for establishing the sufficiency of the KKT conditions are summarized in Table 18.2.
The conditions in Table 18.2 represent only a subset of the conditions in Table 18.1 because a solution space may be convex without satisfying the conditions in Table 18.2.
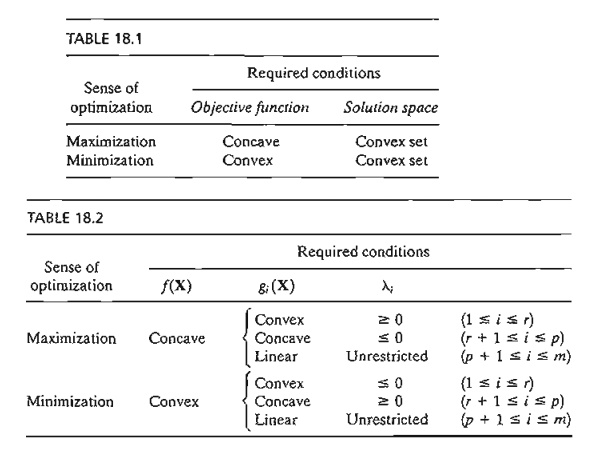
Table 18.2 is valid because the given conditions yield a concave Lagrangean function L(X, S, l) in case of maximization and a convex L(X, S, l) in case of minimization. This result is verified by noticing that if gi( x) is convex, then ligi( x) is convex if li ≥ 0 and concave if li ≤ 0. Similar interpretations can be established for all the remaining conditions. Observe that a linear function is both convex and concave. Also, if a function f is concave, then (-f) is convex, and vice versa.
Example 18.2-5
Consider the following minimization problem:


The solution is x1=1, x2 = 2 , x3=0, l1=l5=0, l3=-2, l4 =-4. Because both f(X) and the solution space g(X) ≤ 0 are convex, L(X, S, l) must be convex and the resulting stationary point yields a global constrained minimum. The KKT conditions are central to the development of the nonlinear programming algorithms in Chapter 19.
PROBLEM SET 18.20
1. Consider the problem:

Show that the KKT conditions are the same as in Section 18.2.2, except that the Lagrange multipliers l are nonpositive.
2. Consider the following problem:

3. Write the KKT necessary conditions for the following problems.

Given f(X) is concave and gi(X)(i = 1,2, ... , m) is a linear function, show that the KKT necessary conditions are also sufficient. Is this result true if gi(X) is a convex nonlinear function for all i? Why?
5. Consider the problem
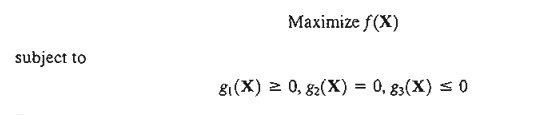
Develop the KKT conditions and give the stipulations under which the conditions are sufficient.
Related Topics