Importance of response quantities

Importance of response quantities

For structural engineers, the deformation of the system or relative displacement with respect to the ground is of great interest. Internal forces, base shear and moments are usually related to displacement. Knowing the total displacement of the mass u_t(t) would be useful in providing a separation between adjacent buildings to prevent their pounding against each other during an earthquake. Pounding is the main cause of damage to several buildings during almost every earthquake. Similarly, the total acceleration is obtained by supporting sensitive equipment and the motion imparted to the equipment can be determined.

1  Response history

For a given earthquake ground motion u˙˙_g ( t ) , the deformation depends on natural period of vibration and damping ratio. Figure 17.8 shows the deformation response of three different systems due to electro ground motion.

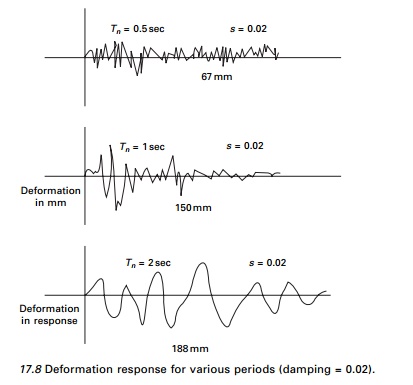
The damping factor is 2%. The only difference among the three systems is the natural periods. It is also seen that the time required for a SDOF systems to complete a cycle of vibration when subjected to earthquake ground motion is also equal to the natural period of displacement. Peak displacement is shown in each case

The longer the natural period, the greater the peak deformation. Figure 17.9 shows the deformation response of three systems to the same ground motion. Vibration period T_n is the same for all but damping is different. From Fig. 17.9 we can observe that systems with more damping respond less than lightly damped systems because the natural periods of three systems are same. Once U(t) is known the base shear V may be calculated (see Fig. 17.10).

Fs(t) = V_b(t) = K U(t)               --- --- 17.12

Equivalent static force is introduced which is a central concept in earthquake response of the structure. At any instant of time t, the force Fs is the static (slowly) applied force that will produce deformation U(t)

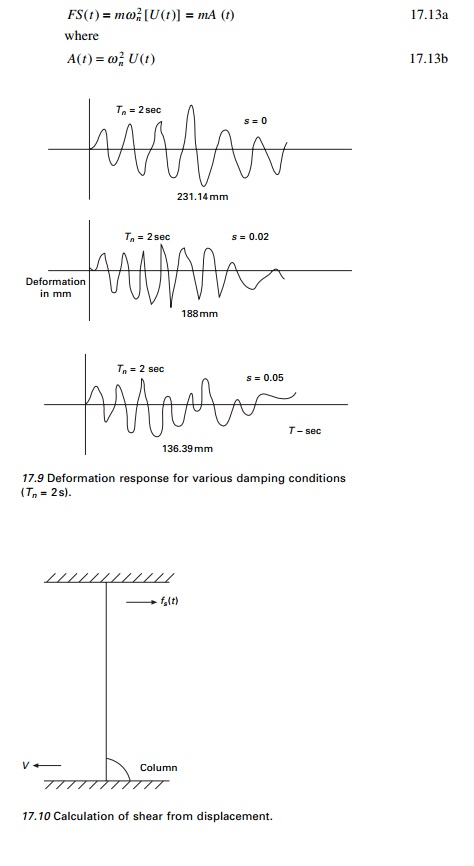
Observe that the equivalent static force is m times A(t), the pseudo-acceleration, not m times total acceleration.

The pseudo-acceleration response can be calculated from the deformation response for the three systems T_n = 0.5: w_n = 12.56: A for (Tn = 0.5) is calculated as (see Fig. 17.8)

For T_n = 1 s A = 0.603g; for T_n = 2 s, A = 0.188g. The pseudo-acceleration graphs are presented in Fig. 17.11.

Thus a static analysis of structure would be required at each time when the response is desired. The base shear and base moment are calculated as

V_b(t) = f_s(t); M_b(t) = hf_s(t)

V_b(t) = mA(t); M_b(t) = V_b(t)h                        17.14