Horizontal and Vertical oscillations of spring

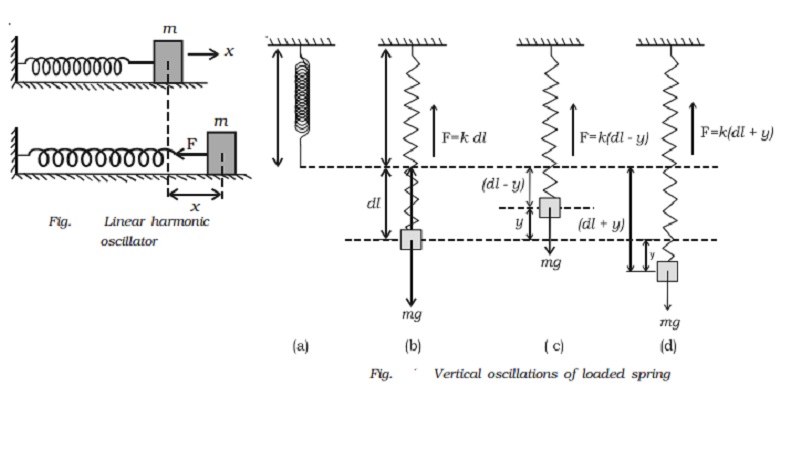
Linear simple harmonic oscillator

The block − spring system is a linear simple harmonic oscillator. All oscillating systems like diving board, violin string have some element of springiness, k (spring constant) and some element of inertia, m.

Horizontal oscillations of spring

Consider a mass (m) attached to an end of a spiral spring (which obeys Hooke?s law) whose other end is fixed to a support as shown in Fig.. The body is placed on a smooth horizontal surface. Let the body be displaced through a distance x towards right and released. It will oscillate about its mean position. The restoring force acts in the opposite direction and is proportional to the displacement.

Restoring force F = −kx

From Newton?s second law, we know that F = ma

∴ ma = −kx

A =  −kx / m

Comparing with the equation of SHM a = −ω²x, we get

ω² = k/m

ω = rt( k/m )

But T = 2π / ω

Time period T = 2π rt(m/k)

∴ Frequency n = 1/T = 1/2 π rt( k/m )

Vertical oscillations of a spring

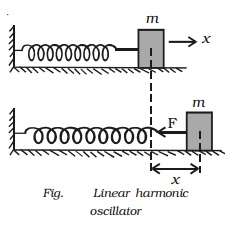
Fig a shows a light, elastic spiral spring suspended vertically from a rigid support in a relaxed position. When a mass ?m? is attached to the spring as in Fig. b, the spring is extended by a small length dl such that the upward force F exerted by the spring is equal to the weight mg.

The restoring force  F = k dl ;       k dl = mg             ...(1)

where k is spring constant. If we further extend the given spring by a small distance by applying a small force by our finger, the spring oscillates up and down about its mean position. Now suppose the body is at a distance y above the equilibrium position as in Fig. c. The extension of the spring is (dl − y). The upward force exerted on the body is k (dl − y) and the resultant force F on the body is

F = k (dl -  y)   - mg = -ky    ???..(2)

The resultant force is proportional to the displacement of the body from its equilibrium position and the motion is simple harmonic.

If the total extension produced is (dl + y) as in Fig. d the restoring force on the body is k (dl + y) which acts upwards.

So, the increase in the upward force on the spring is

k (dl + y) −mg = ky

Therefore if we produce an extension downward then the restoring force in the spring increases by ky in the upward direction. As the force acts in the opposite direction to that of displacement, the restoring force is − ky and the motion is SHM.

F = - ky

 ma = - ky

a = − k/m y ?(3)

a = −ω² y (expression for SHM)

Comparing the above equations, ω = rt(k/m)

But T = 2π / ω = 2π rt(m/k)

From equation (1) mg = k dl

m/k = dl/g

Therefore time period T = 2π rt(dl/g)  ??(6)

Frequency n = 1/2 π rt(g/dl)

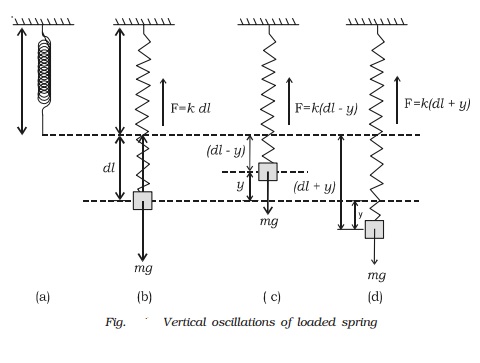
Case 1 : When two springs are connected in parallel

Two springs of spring factors k1 and k2 are suspended from a rigid support as shown in Fig. A load m is attached to the combination.

Let the load be pulled downwards through a distance y from its equilibrium position. The increase in length is y for both the springs but their restoring forces are different.

If F₁ and F₂ are the restoring forces

 F₁ = −k₁y,

 F₂ = −k₂y

∴ Total restoring force = (F₁ + F₂) = −(k₁ + k₂) y

 So, time period of the body is given by

T = 2π rt(m / k +k)

 If k1 = k2 = k

Then, T = 2π rt(m/ 2k)

∴ frequency n = 1/2 π . rt(2k/m)

Case 2 : When two springs are connected in series.

 Two springs are connected in series in two different ways. This arrangement is shown in Fig. a and b.

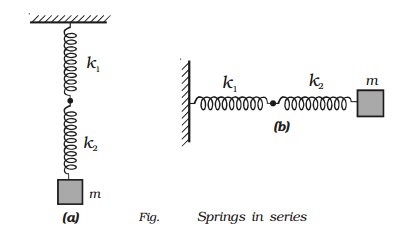
In this system when the combination of two springs is displaced to a distance y, it produces extension y₁ and y₂ in two springs of force constants k₁ and k₂.

F = −k₁ y₁ ;

F = −k₂ y₂

where F is the restoring force.

Total extension, y = y1 + y2 = −F [1/k₁  + 1/k₂]

We know that F = −ky

y= - F/k

From the above equations,

-F/k =  −F [1/k₁  + 1/k₂]

Time period = T = 2π . rt(m(k₁+k₂)/k₁k₂)

frequency n = 1/2 π . rt(k₁k₂ / m(k₁+k₂) )

If both the springs have the same spring constant,

k1 = k2 = k

n= 1/2 π . rt(k/2m)