Theorem, Significance, Illustration, Example, Solution | Mathematics - Fundamental Theorem of Arithmetic | 10th Mathematics : UNIT 2 : Numbers and Sequences
Chapter: 10th Mathematics : UNIT 2 : Numbers and Sequences
Fundamental Theorem of Arithmetic
Fundamental Theorem of Arithmetic
Let us consider the
following conversation between a Teacher and students.
Teacher : Factorise
the number 240.
Malar : 24 ×10
Raghu : 8×30
Iniya : 12×20
Kumar : 15×16
Malar : Whose answer
is correct Sir?
Teacher : All the
answers are correct.
Raghu : How sir?
Teacher : Split each
of the factors into product of prime numbers.
Malar : 2×2×2×3×2×5
Raghu : 2×2×2×2×3×5
Iniya : 2×2×3×2×2×5
Kumar : 3×5×2×2×2×2
Teacher : Good! Now,
count the number of 2’s, 3’s and 5’s.
Malar : I got four
2’s, one 3 and one 5.
Raghu : I got four
2’s, one 3 and one 5.
Iniya : I also got the
same numbers too.
Kumar : Me too sir.
Malar : All of us got
four 2’s, one 3 and one 5. This is very surprising to us.
Teacher : Yes, It should be. Once any number is factorized up to a product of prime numbers, everyone should get the same collection of prime numbers.
This concept leads us
to the following important theorem.
Theorem 4 (Fundamental Theorem of Arithmetic) (without proof)
“Every natural number except 1 can be factorized as a product of primes and this factorization is unique except for the order in which the prime factors are written.”
The fundamental
theorem asserts that every composite number can be decomposed as a product of
prime numbers and that the decomposition is unique. In the sense that there is
one and only way to express the decomposition as product of primes.
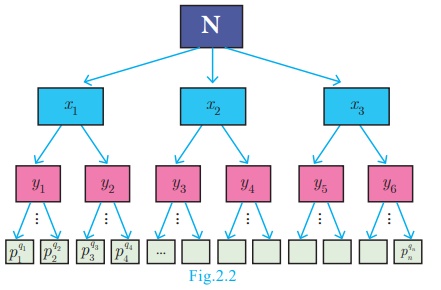
In general, we
conclude that given a composite number N, we decompose it uniquely in the form N
= p1q1 × p2q2 × p3q3 × …… × pnqn where p1,
p2, p3,……. ,pn
are primes and q1, q2, q3, …. qn
are natural.
First, we try to factorize N into its factors. If all the factors are themselves primes then we can stop. Otherwise, we try to further split the factors which are not prime. Continue the process till we get only prime numbers.
Illustration
For example, if we try
to factorize32760 we get
32760 = 2 × 2 × 2 × 3
× 3 × 5 × 7 ×13
= 23 × 32
× 51 × 71 ×131
Thus, in whatever way
we try to factorize 32760, we should finally get three 2’s, two 3’s, one 5, one
7 and one 13.
The fact that “Every
composite number
can be written uniquely as the product of power of
primes” is called Fundamental Theorem of
Arithmetic.
Significance of the Fundamental Theorem of Arithmetic
The fundamental theorem about natural numbers except 1, that we have stated above has several applications, both in Mathematics and in other fields. The theorem is vastly important in Mathematics, since it highlights the fact that prime numbers are the ‘Building Blocks’ for all the positive integers. Thus, prime numbers can be compared to atoms making up a molecule.
1. If a prime number p
divides ab then either p divides a or p divides b.
That is p divides at
least one of them.
2. If a composite number n
divides ab, then n neighter divide a nor b.
For example, 6 divides 4 × 3 but 6 neither divide 4 nor 3.
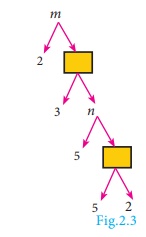
Example 2.7
In the given factor
tree, find the numbers m and n.
Solution
Value of the first box
from bottom = 5 × 2 = 10
Value of n = 5
×10 = 50
Value of the second
box from bottom = 3 × 50 = 150
Value of m = 2
×150 = 300
Thus, the required
numbers are m = 300, n = 50
Example 2.8
Can the number 6n
, n being a natural number end with the digit 5? Give reason for
your answer.
Solution
Since 6n=
(2 × 3)n = 2n × 3n
2 is a factor of 6n . So, 6n is always even. But any number whose last digit is 5 is always odd. Hence, 6n cannot end with the digit 5
Example 2.9
Is 7 × 5 × 3 × 2 + 3 a
composite number? Justify your answer.
Solution
Yes, the given number
is a composite number, because
7 × 5 × 3 × 2 + 3 = 3
× (7 × 5 × 2 + 1) = 3 × 71
Since the given number
can be factorized in terms of two primes, it is a composite number.
Example 2.10
‘a’ and ‘b’
are two positive integers such that ab ×ba =
800. Find ‘a’ and ‘b’.
Solution The number 800 can be
factorized as
800 = 2 × 2 × 2 × 2 ×
2 × 5 × 5 = 25 × 52
Hence, ab
×ba = 25 × 52
This implies that a = 2 and b = 5 (or) a = 5 and b = 2
Related Topics