Fluids in Motion

Fluids in Motion

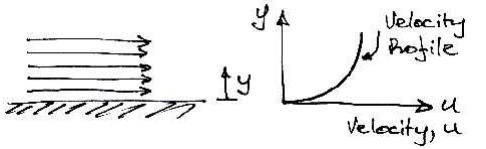
For example, consider the fluid shown flowing along a fixed surface. At the surface there will be little movement of the fluid (it will 'stick' to the surface), whilst furtheraway from the surface the fluid flows faster (has greater velocity):

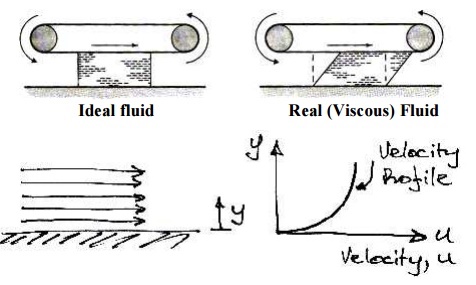
If one layer of is moving faster than another layer of fluid, there must be shear forcesacting between them. For example, if we have fluid in contact with a conveyor beltthat is moving we will get the behaviour shown:

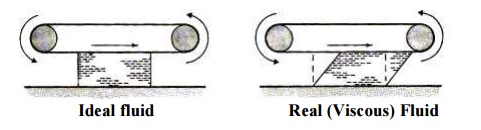
When fluid is in motion, any difference in velocity between adjacent layers has the same effect as the conveyor belt does.

Therefore, to represent real fluids in motion we must consider the action of shear forces

Consider the small element of fluid shown, which is subject to shear force and has a dimension sinto the page. The force F acts over an area A = BC× s. Hence we have a shear stress applied:

Any stress causes a deformation, or strain, and a shear stress causes a shear strain. This shear strain is measured by the angle ? . Remember that a fluid continuously deforms when under the action of shear. This is different to a solid: a solid has a single value of ? for each value of ? . So the longer a shear stress is applied to a fluid, the more shear strain occurs. However, what is known from experiments is that the rate of shear strain (shear strain per unit time) is related to the shear stress:

We need to know the rate of shear strain. From the diagram, the shear strain is:

If we suppose that the particle of fluid at E moves a distance x in time t, then, using S = R? for small angles, the rate of shear strain is:

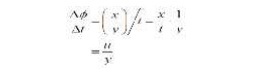
Where u is the velocity of the fluid. This term is also the change in velocity with height. When we consider infinitesimally small changes in height we can write this in differential form, du/ dy . Therefore we have:

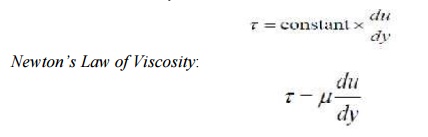
Newton's Law of Viscosity:

Generalized Laws of Viscosity

We have derived a law for the behaviour of fluids - that of Newtonian fluids. However, experiments show that there are non-Newtonian fluids that follow a generalized law of viscosity:

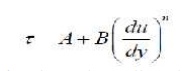
Where A, B and n are constants found experimentally. When plotted these fluids show much different behaviour to a Newtonian fluid:

Behaviour of Fluids and Solids

In this graph the Newtonian fluid is represent by a straight line, the slope of which is ? . Some of

the other fluids are:

Plastic: Shear stress must reach a certain minimum before flow commences.

Pseudo-plastic: No minimum shear stress necessary and the viscosity decreases with rate of shear, e.g. substances like clay, milk and cement.

Dilatant substances; Viscosity increases with rate of shear, e.g. quicksand.

Viscoelastic materials: Similar to Newtonian but if there is a sudden large change in shear they behave like plastic.

Solids: Real solids do have a slight change of shear strain with time, whereas ideal solids (those we idealise for our theories) do not. Lastly, we also consider the ideal

fluid. This is a fluid which is assumed to have no viscosity and is very useful for developing theoretical solutions. It helps achieve some practically useful solutions.

Properties

Further Reading

Here we consider only the relevant properties of fluids for our purposes. Find out about

surface tension and capillary action elsewhere. Note that capillary action only features in

pipes of

? 10 mm diameter.