Theorem, Example, Solution - Euclid’s Division Lemma | 10th Mathematics : UNIT 2 : Numbers and Sequences
Chapter: 10th Mathematics : UNIT 2 : Numbers and Sequences
Euclid’s Division Lemma
Euclid’s Division Lemma
Euclid, one of the
most important mathematicians wrote an important book named “Elements” in 13
volumes. The first six volumes were devoted to Geometry and for this reason,
Euclid is called the “Father of Geometry”. But in the next few volumes, he made
fundamental contributions to understand the properties of numbers. One among
them is the “Euclid’s Divison Lemma”. This is a simplified version of the long
division process that you were performing for division of numbers in earlier
classes.
Le us now discuss
Euclid’s Lemma and its application through an Algorithm termed as “Euclid’s
Division Algorithm”.
Lemma is an auxiliary
result used for proving an important theorem. It is usually considered as a
mini theorem.
Theorem 1: Euclid’s Division Lemma
Let a and b (a
> b) be any two positive integers. Then, there exist unique
integers q and r such that a = bq + r, 0 ≤ r
< b.
Note
·
The remainder is always less than the divisor.
·
If r = 0 then a =
bq so b divides a.
·
Similarly, if b divides a then a = bq
Example 2.1
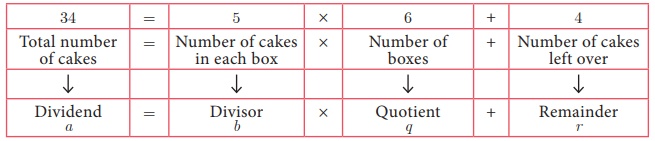
We have 34 cakes. Each
box can hold 5 cakes only. How many boxes we need to pack and how many cakes are
unpacked?
Solution
We see that 6 boxes
are required to pack 30 cakes with 4 cakes left over. This distribution of
cakes can be understood as follows:
NOTE
·
The above lemma is nothing but a restatement of the long
division process, the integers q and r are called quotient and
remainder respectively.
·
When a positive integer is divided by 2 the remainder is either
0 or 1. So, any positive integer will of the form 2k, 2k+1 for
some integer k.
Euclid’s Division
Lemma can be generalised to any two integers.
Generalised form of Euclid’s division lemma.
If a and b are any two integers then there exist unique integers q and r such that a = bq +r , where 0 ≤|r| < |b|
Example 2.2
Find the quotient and
remainder when a is divided by b in the following cases (i) a =
−12 , b = 5 (ii) a = 17 , b = −3 (iii)a = −19 , b
= −4
Solutions
(i) a = −12 , b = 5
By Euclid’s division
lemma
a = bq + r ,
where 0 ≤ r < |b|
−12 = 5 × (−3) + 3 : 0 ≤ r < |5|
Therefore, Quotient q
= −3, Remainder r = 3
(ii) a = 17 b = −3
By Euclid’s division
lemma
a = bq + r ,
where 0 ≤ r < |b|
17 = (−3)×(−5) + 2 ….. 0
≤ r < |-3|
Therefore Quotient q
= −5,
Remainder r = 2
(iii) a = −19, b = −4
By Euclid’s division
lemma
a = bq + r ,
where 0 ≤ r < |b|
−19 = (−4)×(5) + 1 ….. 0
≤ r < |-4|
Therefore Quotient q
= 5, Remainder r = 1 .
Example 2.3
Show that the square
of an odd integer is of the form 4q + 1 , for some integer q.
Solution
Let x be any
odd integer. Since any odd integer is one more than an even integer, we have x
= 2k + 1 , for some integer k.
x2 = (2k + 1)2
= 4k2
+ 4k + 1
= 4k(k +
1) + 1
= 4q + 1 ,
where q = k(k + 1) is some integer.
Related Topics