Definition of the Dual Problem

DEFINITION OF THE DUAL PROBLEM

The dual problem is an LP defined directly and systematically from the primal (or original) LP model. The two problems are so closely related that the optimal solution of one problem automatically provides the optimal solution to the other.

In most LP treatments, the dual is defined for various forms of the primal depending on the sense of optimization (maximization or minimization), types of constraints (≤,≥,=) and orientation of the variables (nonnegative or unrestricted). This type of treatment is somewhat confusing, and for this reason we offer a single definition that automatically subsumes all forms of the primal.

Our definition of the dual problem requires expressing the primal problem in the equation form presented in Section 3.1 (all the constraints are equations with nonnegative right-hand side and all the variables are nonnegative). This requirement is consistent with the format of the simplex starting tableau. Hence, any results obtained from the primal optimal solution will apply directly to the associated dual problem.

To show how the dual problem is constructed, define the primal in equation form as follows:

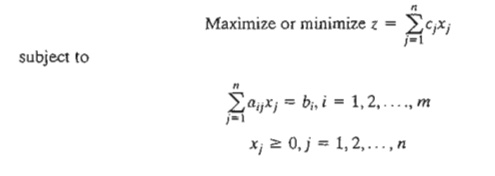
The variables x_j, j = 1,2, ... , n, include the surplus, slack, and artificial variables, if any. Table 4.1 shows how the dual problem is constructed from the primal. Effectively,

we have

1.     A dual variable is defined for each primal (constraint) equation.

2.     A dual constraint is defined for each primal variable.

3.     The constraint (column) coefficients of a primal variable define the left-hand-side coefficients of the dual constraint and its objective coefficient define the right-hand side.

4.     The objective coefficients of the dual equal the right-hand side of the primal con-straint equations.

TABLE 4.1      Construction of the Dual from the Primal

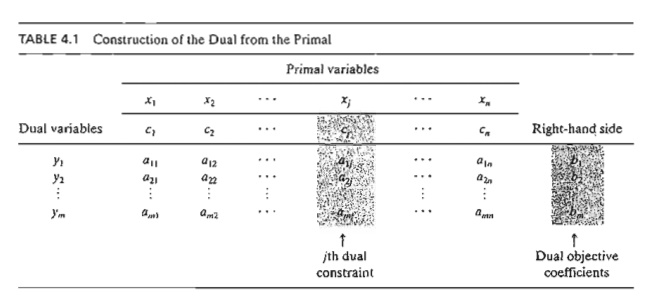
The rules for determining the sense of optimization (maximization or minimization), the type of the constraint( ≤, ≥, or =), and the sign of the dual variables are summarized in Table 4.2. Note that the sense of optimization in the dual is always opposite to that of the primal. An easy way to remember the constraint type in the dual (i.e., ≤ or ≥) is that if the dual objective is minimization (i.e., pointing down), then the constraints are all of the type ≥ (i.e., pointing up). The opposite is true when the dual objective is maximization.

The following examples demonstrate the use of the rules in Table 4.2 and also show that our definition incorporates all forms of the primal automatically.

The first and second constraints are replaced by an equation. The general rule in this case is that an unrestricted primal variable always corresponds to an equality dual constraint. Conversely, a primal equation produces an unrestricted dual variable, as the first primal constraint demonstrates.

Summary of the Rules for Constructing the Dual. The general conclusion from the preceding examples is that the variables and constraints in the primal and dual problems are defined by the rules in Table 4.3. It is a good exercise to verify that these explicit rules are subsumed by the general rules in Table 4.2.

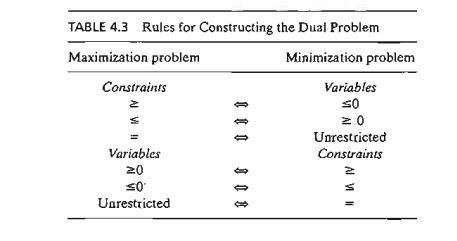
Note that the table does not use the designation primal and dual. What matters here is the sense of optimization. If the primal is maximization, then the dual is minimization, and vice versa.

PROBLEM SET 4.1A

1. In Example 4.1-1, derive the associated dual problem if the sense of optimization in the primal problem is changed to minimization.

*2.  In Example 4.1-2, derive the associated dual problem given that the primal problem is augmented with a third constraint, 3x_l + x₂ = 4.

3. In Example 4.1-3, show that even if the sense of optimization in the primal is changed to minimization, an unrestricted primal variable always corresponds to an equality dual constraint.

4. Write the dual for each of the following primal problems:

*5. Consider Example 4.1-1. The application of the simplex method to the primal requires the use of an artificial variable in the second constraint of the standard primal to secure a starting basic solution. Show that the presence of an artificial primal in equation form variable does not affect the definition of the dual because it leads to a redundant dual constraint.

6. True or False?

a.       The dual of the dual problem yields the original primal.

b.       If the primal constraint is originally in equation form, the corresponding dual vari-able is necessarily unrestricted.

c.       If the primal constraint is of the type ≤, the corresponding dual variable will be non-negative (nonpositive) if the primal objective is maximization (minimization).

d.       If the primal constraint is of the type ≥, the corresponding dual variable will be non-negative (nonpositive) if the primal objective is minimization (maximization).

e.       An unrestricted primal variable will result in an equality dual constraint.