Cutting-Plane Algorithm

Cutting-Plane Algorithm

As in the B&B algorithm, the cutting-plane algorithm also starts at the continuous optimum LP solution. Special constraints (called cuts) are added to the solution space in a manner that renders an integer optimum extreme point. In Example 9.2-2, we first demonstrate graphically how cuts are used to produce an integer solution and then implement the idea algebraically. 

Example 9.2-2

Consider the following ILl'.

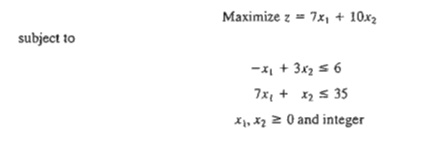
The cutting-plane algorithm modifies the solution space by adding cuts that produce an optimum integer extreme point. Figure 9.10 gives an example of two such cuts.

Initially, we start with the continuous LP optimum z = 66(1/2), x₁  = 4(1/2), x₂  =  3(4/7). Next, we add cut I, which produces the (continuous) LP optimum solution z = 62, x₁ = 4(4/7), x₂ = 3. Then, we add cut II, which, together with cut I and the original constraints, produces the LP optimum z = 58, x_l = 4, x₂ = 3. The last solution is all integer, as desired.

The added cuts do not eliminate any of the original feasible integer points, but must pass through at least one feasible or infeasible integer point. These are basic requirements of any cut.

FIGURE 9.10

Illustration of the use of cuts in ILP

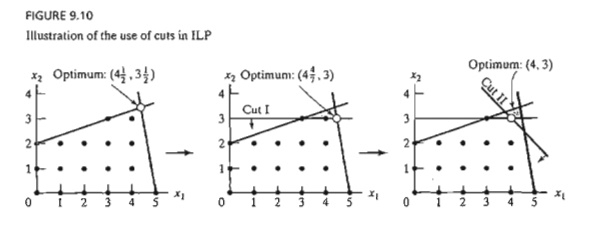
It is purely accidental that a 2-variable problem used exactly 2 cuts to reach the optimum integer solution. In general, the number of cuts, though finite, is independent of the size of the problem, in the sense that a problem with a small number of variables and constraints may re-quire more cuts than a larger problem.

Next, we use the same example to show how the cuts are constructed and implemented algebraically.

Given the slacks x3 and x4 for constraints 1 and 2, the optimum LP tableau is given as

The optimum continuous solution is z = 66(1/2), x₁= 4(1/2), x₂ = 3(1/2), x₃ = 0, x₄ = 0. The cut is developed under the assumption that all the variables (including the slacks x₃ and x₄) are integer. Note also that because all the original objective coefficients are integer in this example, the value of z is integer as well.

The information in the optimum tableau can be written explicitly as

A constraint equation can be used as a source row for generating a cut, provided its right-hand side is fractional. We also note that the z-equation can be used as a source row because z happens to be integer in this example. We will demonstrate how a cut is generated from each of these source rows, starting with the z-equation.

First, we factor out all the noninteger coefficients of the equation into an integer value and a fractional component, provided that the resulting fractional component is strictly positive. For example,

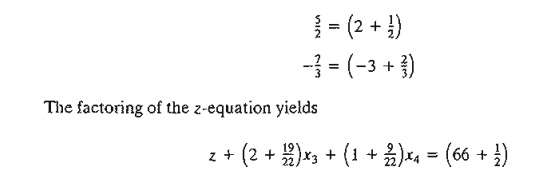
Moving all the integer components to the left-hand side and all the fractional components to the right-hand side, we get

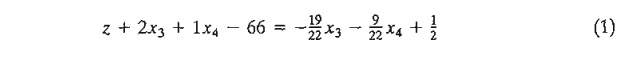
Because x₃ and x₄ are nonnegative and all fractions are originally strictly positive, the right-hand side must satisfy the following inequality:

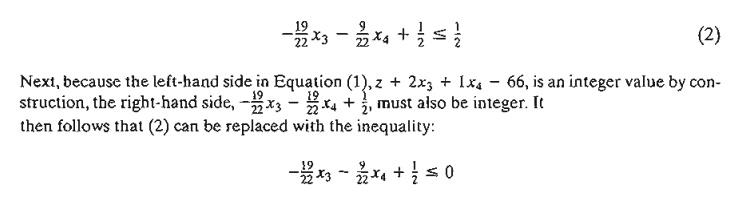
This result is justified because an integer value ≤ 1/2 must necessarily be ≤ 0 .

The last inequality is the desired cut and it represents a necessary (but not sufficient) condition for obtaining an integer solution. It is also referred to as the fractional cut because all its co-efficients are fractions.

Because x₃ = x₄ = 0 in the optimum continuous LP tableau given above, the current continu-ous solution violates the cut (because it yields 1/2 ≤ 0). Thus, if we add this cut to the optimum tableau, the resulting optimum extreme point moves the solution toward satisfying the integer requirements.

Before showing how a cut is implemented in the optimal tableau, we will demonstrate how cuts can also be constructed from the constraint equations. Consider the x₁-row:

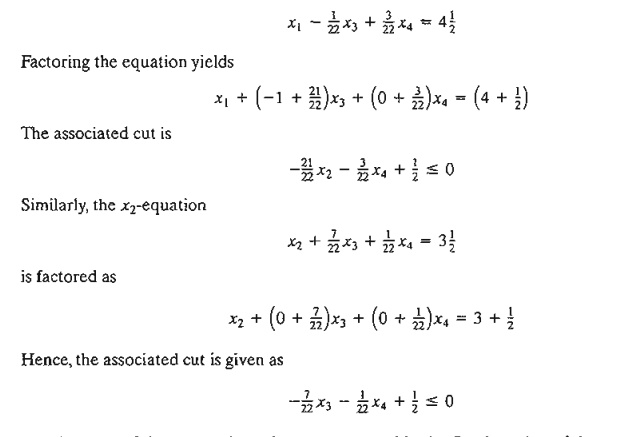
Anyone of three cuts given above can be used in the first iteration of the cutting-plane a1gorithm. It is not necessary to generate all three cuts before selecting one.

Arbitrarily selecting the cut generated from the x₂-row, we can write it in equation form as

This constraint is added to the LP optimum tableau as follows:

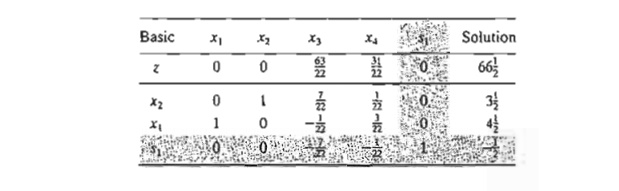
The tableau is optimal but infeasible. We apply the dual simplex method (Section 4.4.1) to recover feasibility, which yields

The last solution is still noninteger in x_l and x₃. Let us arbitrarily select x_l as the next source row-that is,

The dual simplex method yields the following tableau:

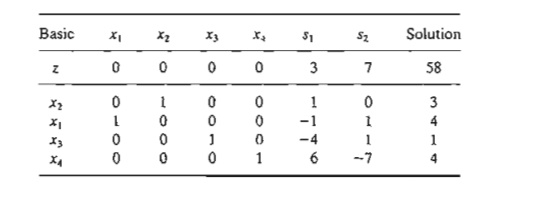
The optimum solution (x_l = 4, x₂ = 3, z = 58) is all integer. It is not accidental that all the coefficients of the last tableau are integers, a property of the implementation of the fractional cut.

Remarks. It is important to point out that the fractional cut assumes that all the variables, including slack and surplus, are integer. This means that the cut deals with pure integer problems only. The importance of this assumption is illustrated by an example.

Consider the constraint

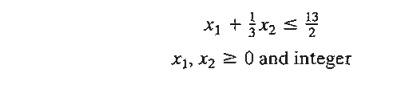
From the standpoint of solving the associated ILP, the constraint is treated as an equation by using the nonnegative slack s_l-that is,

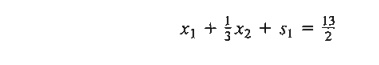
The application of the fractional cut assumes that the constraint has a feasible integer solution in all x_l, x₂, and s_l. However, the equation above will have a feasible integer solution in x_l and x₂ only if x₁ is noninteger. This means that the cutting-plane algorithm will show that the problem has no feasible integer solution, even though the variables of concern, x_l and x₂, can assume feasible integer values.

There are two ways to remedy this situation.

1. Multiply the entire constraint by a proper constant to remove all the fractions. For example, multiplying the constraint above by 6, we get

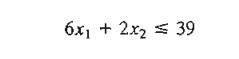
Any integer solution of x₁ and x₂ automatically yields integer slack. However, this type of conversion is appropriate for only simple constraints, because the magnitudes of the integer coefficients may become excessively large in some cases.

2. Use a special cut, called the mixed cut, which allows only a subset of variables to assume integer values, with all the other variables (including slack and surplus) remaining continuous. The details of this cut will not be presented in this chapter (see Taha, 1975, pp. 198-202).

PROBLEM SET 9.2B

1. In Example 9.2-2, show graphically whether or not each of the following constraints can form a legitimate cut:

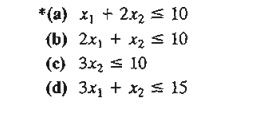
2. In Example 9.2-2, show graphically how the following two (legitimate) cuts can lead to the optimum integer solution:

3. Express cuts I and II of Example 9.2-2 in terms of X_l and X₂ and show that they are the same ones used graphically in Figure 9.10.

4. In Example 9.2-2, derive cut II from the x3-row. Use the new cut to complete the solution of the example.

5. Show that, even though the following problem has a feasible integer solution in x₁ and x₂, the fractional cut would not yield a feasible solution unless all the fractions in the con-straint were eliminated.

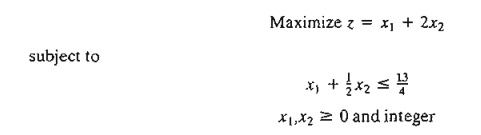
6. Solve the following problems by the fractional cut, and compare the true optimum integer solution with the solution obtained by rounding the continuous optimum.

*(a) Maximize z = 4XI + 6X2 + 2X3 subject to