Conducting Materials

Conducting Materials

1 Introduction

1.1 Classical free electron theory

1.2 Quantum free electron theory

1.3  Zone theory (or) Band theory

2 Assumptions (postulates) of Classical free electron theory

3 Basic terms involved in the free electron theory

4 Success or uses of Classical free electron theory

5 Drawbacks of Classical free electron theory

6 Expression for Electrical Conductivity

6.1 Expression for electrical conductivity

6.2 Correct expression for electrical conductivity of conductors

7 Thermal conductivity (K)

7.1 Expression for thermal conductivity (K) of an electron

8 Wiedemann-franz Law

8.1 Derivation

8.2 By Quantum theory

9 Quantum Free Electron Theory

9.1 Assumptions (Postulates) of Quantum free electron theory

9.2 Advantages of Quantum free electron theory

9.3 Drawbacks of Quantum free electron theory

10 Fermi – Dirac Distribution Function

10.1 Effect of Temperature on Fermi Function

10.2 Fermi level, Fermi Energy and their importance

11 Density of States

11.1 Carrier concentration in metals

11.2 Average energy of an electron at 0K

12 Work Function

12.1 Explanation

1  INTRODUCTION

The electron theory of solids explains the structures and properties of solids through their electronic structure. This theory is applicable to all solids both metals and non metals. This theory also explains the bending in solids behavior of conductors and insulators, electrical and thermal conductivities of solids, elasticity and repulsive forces in solids etc,.. The theory has been developed in three main stages.

1.1  Classical free electron theory

This theory was developed by Drude and Lorentz. According to this theory, a metal consists of electrons which are free to move about in the crystal molecules of a gas it contains mutual repulsion between electrons is ignored and hence potential energy is taken as zero. Therefore the total energy of the electron is equal to its kinetic energy.

1.2  Quantum free electron theory

Classical free electron theory could not explain many physical properties. In classical free electron theory, we use Maxwell-Boltzman statics which permits all free electrons to gain energy. In Somerfield developed a new theory, in which he retained some of the features of classical free electron theory included quantum mechanical concepts and Fermi-Dirac statistics to the free electrons in the metals. This theory is called quantum free electron theory. Quantum free electron theory permits only a few electrons to gain energy.

1.3  Zone theory (or) Band theory

Bloch developed the theory in which the electrons move in a periodic field provided by the Lattice concept of holes, origin of Band gap and effective mass of electrons are the special features of this theory of solids. This theory also explains the mechanism of super conductivity based on band theory.

ASSUMPTIONS (POSTULATES) OF CLASSICAL FREE

ELECTRON THEORY

A Solid metal has nucleus with revolving electrons. The electrons move freely like molecules in a gas.

The free electrons move in a uniform potential field due to the ions fixed in the lattice.

In the absence of electric field (E=0), the free electrons move in random directions and collide with each other. During this collision no loss of energy is observes since the collisions are elastic as shown in figure.

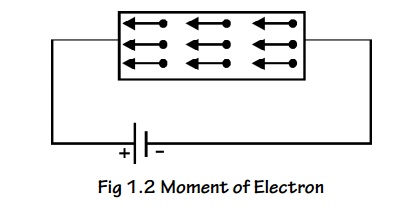
When the presence of electric field ( _{E 0} ) the free electrons are accelerated in the direction opposite to the direction of applied electric field, as shown in figure.

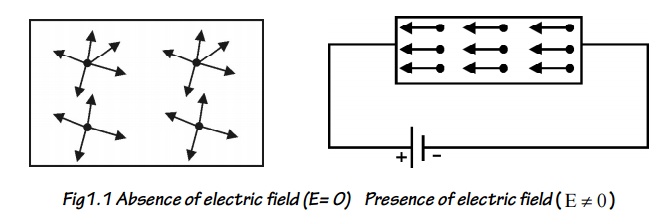
Fig1.1 Absence of electric field (E= 0)  Presence of electric field ( _{E 0} )

Since the electrons are assumed to be perfect gas, they obey the laws of classical theory of gases.

Classical free electrons in the metal obey Maxwell-Boltzmann statistics.

3 BASIC TERMS INVOLVED IN THE FREE ELECTRON THEORY

1. Drift Velocity (V_d)

The drift velocity is defined as the average velocity acquired by the free electron in particular direction, due to the applied electric field.

2. Mobility 

The mobility is defined as the drift velocity (V_d) acquired by the electron per unit electric field (E).

3. Mean free path

The average distance travelled by a electron between two successive collision is called mean free path.

4. Mean collision time  (or) Collision time

It is the time taken by the free electron between two successive collision.

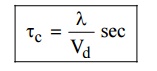
5. Relaxation time

It is the time taken by the electron to reach equilibrium position from disturbed position in the presence of electric field.

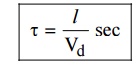
Where l is the distance travelled by the electron. The value of relaxation time is of the order of 10^–14 sec.

6. Band gap (E_g)

Band gap is the energy difference between the minimum energy of conduction band and the maximum energy of valence band.

7. Current density (J)

It is defined as the current per unit area of cross section of an imaginary plane holded normal to the direction of the flow of current in a current carrying conductor.

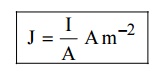
4 SUCCESS OR USES OF CLASSICAL FREE ELECTRON

THEORY

It is used to verify Ohm’s law.

It is used to explain electrical conductivity ( σ) and thermal conductivity of (K) of metals.

It is used to derive Widemann-Franz law.

It is used to explain the optical properties of metal.

5 DRAWBACKS OF CLASSICAL FREE ELECTRON THEORY

It is a macroscopic theory.

According to classical free electron theory, all the free electrons will absorb energy, but the quantum free electron theory states that only few electrons will absorb energy.

This theory cannot explain the Compton effect, Photo-electric effect, para-magnetism and ferromagnetism, etc.,

This theory cannot explain the electrical conductivity of semiconductors and insulators.

Dual nature of light radiation cannot be explained.

The theoretical and experimental values of specific heat and electronic specific heat are not matched.

The Lorentz number obtained by classical theory does not have good agreement with experimental value and theoritical value, it is rectified by quantum theory.

6  EXPRESSION FOR ELECTRICAL CONDUCTIVITY

Definition

The electrical conductivity is defined as the quantity of electricity flowing per unit area per unit time at a constant potential gradient.

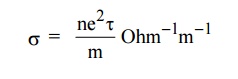
6.1  Expression for electrical conductivity

When an electric field (E) is applied to a conductor the free electrons are accelerated and give rise to current (I) which flows in the direction of electric filed flows of charges is given in terms of current density.

Let ‘n’ be the number of electrons per unit volume and ‘e’ be the charge of the electrons.

The current flowing through a conductor per unit area in unit time (current density) is given by

The negative sign indicates that the direction of current is in opposite direction to the movement of electron.

Due to the applied electric field, the electrons acquire an acceleration ‘a’ can be given by

When an electric field of strength (E) is applied to the conductor, the force experienced by the free electrons in given by

From Newton’s second Law of motion, the force acquired by the electrons can be written as

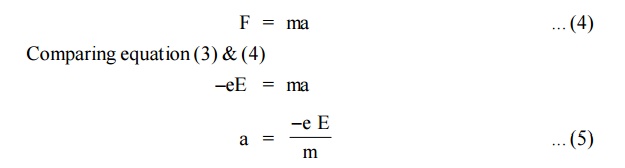
Now, substituting the value of ‘a’ from the equation (2),we get

The electrical conductivity of a material is directly proportional to the free electron concentration in the material.

6.2 Correct expression for electrical conductivity of conductors

By using the classical free electron theory, quantum free electron theory and band theory of solids we can get,

Where m*-  effective mass of free electron

Electrical conductivity

Relaxation time

Number of electrons

7 THERMAL CONDUCTIVITY (K)

Definition

The thermal conductivity is defined as the amount of heat flowing through an unit area per unit temperature gradient.

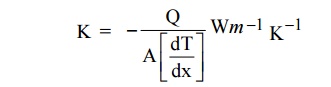
The negative sign indicates that heat flows hot end to cold end.

Where K is the thermal conductivity of metal. Q is the amount of heat energy.

In general, the thermal conductivity of a material is due to the presence of lattice vibrations (ie., photons and electrons). Hence the total thermal conduction can be written as.

7.1  Expression for thermal conductivity (K) of an electron

Consider a metal bar with two planes A and B separated by a distance ‘ ’ from C. Here T₁ is hot end and T₂ is cold end. ie., T₁ > T₂

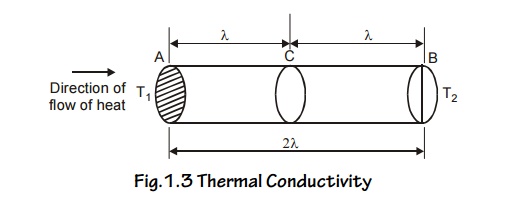
Fig.1.3 Thermal Conductivity

Let ‘n’ be the number of conduction electrons and ‘v’ be the velocity of the electrons. K_B is the Boltzmann constant

From kinetic theory of gases

Fig.1.4 moment of electron field

Let as assume that there is equal probability for the electrons to move in all the six directions. Each electrons travels with thermal velocity ‘V’ and ‘n’ is the free electron density then on average of 1/6 nv electron will travel in any one direction.

No. of electrons crossing per unit area in unit time at C

8  WIEDEMANN-FRANZ LAW

Statement

The ratio between the thermal conductivity (K) and electrical conductivity (σ) of a metal is directly proportional to the absolute temperature of the metal.

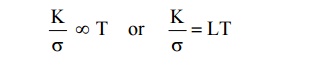
Where L is called Lorentz number, the value of L is 2.44 × 10^–8 W K^–2 (as per Quantum Mechanical value).

8.1  Derivation

By Classical theory, we can drive Widemann-Franz law using the expressions for electrical and thermal conductivity of metals.

The expression for thermal conductivity

Thus, it is proved that the ratio of thermal conductivity and electrical conductivity of a metal is directly propotional to the absolute temperature of the metal.

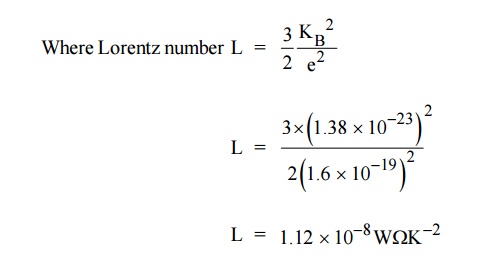
It is found that the classical value of Lorentz number is only one half of the experimental value (2.44 × 10^–8 W K^–2). The discrepancy of L value is the failure of the classical theory (Experimental and Theoretical). This can be rectified by quantum theory.

8.2  By Quantum theory

By Quantum theory the mass ‘m’ is replaced by effective mass m*

According to Quantum theory, the expression for thermal conductivity is modified by considering the electron specific heat as

This is gives the correct value of Lorentz number and it in good agreement with the experiment value.

9  QUANTUM FREE ELECTRON THEORY

The failure of classical free electron theory paved this way for Quantum free electron theory. It was introduced by Sommer field in 1928. This theory is based on making small concepts. This theory was proposed by making small changes in the classical free electron theory and by retaining most of the postulates of the classical free electron theory.

9.1 Assumptions (Postulates) of Quantum free electron theory

In a metal the available free electrons are fully responsible for electrical conduction.

The electrons move in a constant potential inside the metal. They cannot come out from the metal surface have very high potential barrier.

Electrons have wave nature, the velocity and energy distribution of the electron is given by Fermi-Dirac distribution function.

The loss of energy due to interaction of the free electron with the other free electron.

Electron’s distributed in various energy levels according to Pauli Exclusion Principle.

9.2 Advantages of Quantum free electron theory

This theory explains the specific heat capacity of materials.

This theory explains photo electric effect, Compton Effect and block body radiation. etc.

This theory gives the correct mathematical expression for the thermal conductivity of metals.

9.3 Drawbacks of Quantum free electron theory

This theory fails to distinguish between metal, semiconductor and Insulator.

It also fails to explain the positive value of Hall Co-efficient.

According to this theory, only two electrons are present in the Fermi level and they are responsible for conduction which is not true.

10 FERMI – DIRAC DISTRIBUTION FUNCTION

Statement

It is an expression for the distribution of electrons among the energy levels as a function of temperature, the probability of finding an electron in a particular energy state of energy E is given by

Where,            E_F - Fermi energy (highest energy level of an electron)

K_B - Boltzmann’s constant

T -   Absolute temperature

10.1 Effect of Temperature on Fermi Function

Case 1:

AT = 0 K and E < E_F

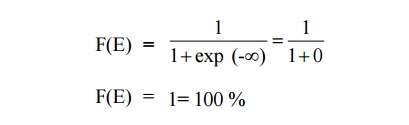
It means that 100% probability for the electrons to occupy the energy level below the Fermi energy level.

Case 2:

AT = 0 K and E > E_F

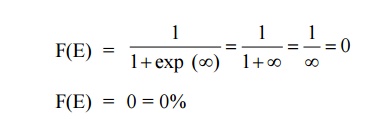
It means that 0% probability (electron) for the electrons to occupy the energy level above the Fermi energy level.

Case 3 :

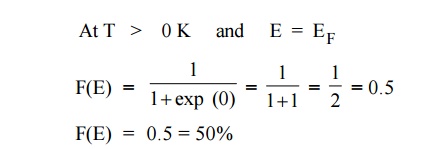
It means that 50% probability for the electrons to occupy the Fermi energy level. (above Fermi energy level are empty and below Fermi energy level are filled). At 0 K energy states above E_F are empty and below E_F are filled.

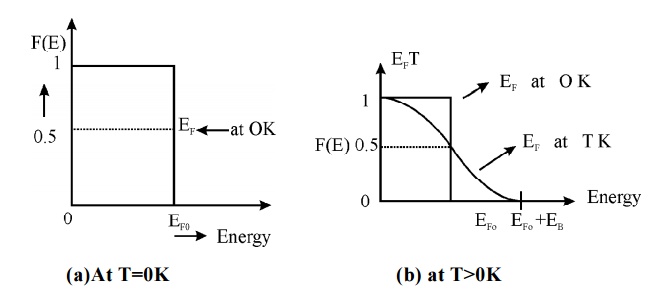
Fig.1.5 Fermi Dirac distribution function

10.2 Fermi level, Fermi Energy and their importance

These are defined as the highest energy level filled by the electrons in that energy level with higher energy values.

Fermi level :  The Fermi level is the highest reference energy level of a particle at absolute zero.

Importance :  It is the reference energy level which separates the filled energy levels and vacant energy levels.

Fermi energy (EF) : The Fermi energy is the maximum energy of the quantum state corresponding to Fermi energy level at absolute zero.

Importance :  Fermi energy determines the energy of the particle at any temperature.

11 DENSITY OF STATES

A parameter of interest in the study of conductivity of metals and semiconductors is the density of states.

The Fermi function F(E) gives only the probability of filling up of electrons in a given energy state. It does not give the information about the number of electrons that can be filled in a given energy state, to know that we should know the number of available energy states called density of states.

Density of states is defined the as the number of energy states per unit volume in an energy interval of a metal. It is use to calculate the number of charge carriers per unit volume of any solid.

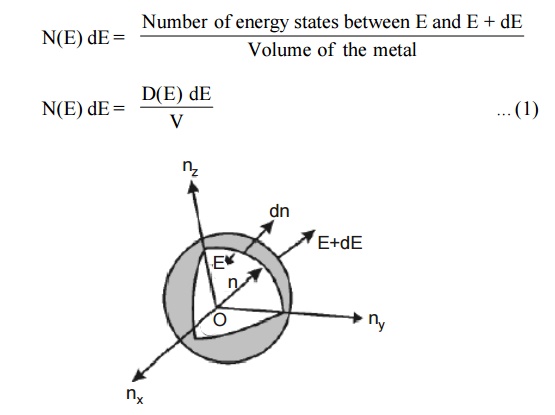
Fig.1.6 Positive octant of n space

Let us constant a sphere of radius “n” in space with quantum numbers n_n ^, n_y and n_z

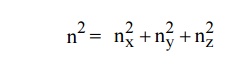
The sphere is further divided into many shells represents a particular combination of quantum numbers and represents particular energy value.

Therefore, the number of energy states within a sphere of radius

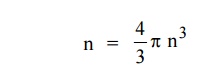
Let us consider two energy values E and E + dE can be found by finding the number of energy states between the shells of radius n and n+ dn from the origin. Since the quantum numbers are positive integers, n values can be defined only in the positive octant of the n – space.

The number of available energy states within the sphere of radius “n” due to one octant.

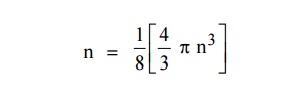
Similarly the number of available energy states within the sphere of radius n+dn corresponding energy.

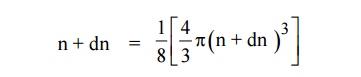
The number of available energy states between the shells of radius n and n + dn (or) between the energy levels E and E + dE

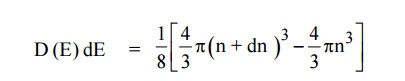
The number of available energy states between the energy interval dE

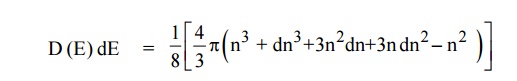
Since the higher powers of dn is very small, dn² and dn³ terms can be neglected.

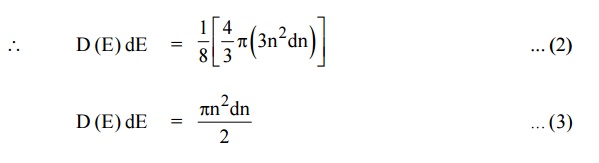
We know that the allowed energy values is

Differentiating equation (4) with respect to ‘n’

Each electron energy level can accommodate two electrons as per Pauli’s exclusion principle. (Spin up and Spin down = 2 (e) × density of states).

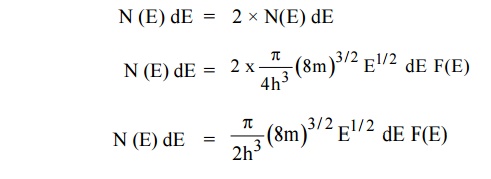
11.1 Carrier concentration in metals

Let N(E) dE represents the number of filled energy states between the interval of energy dE, normally all the energy states will not be filled

dN = N (E) dE F(E)

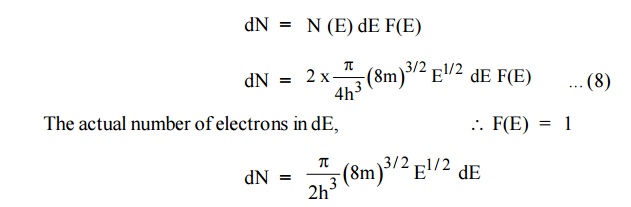
Normally all the states are not filled states, filling of electrons is a given energy state is given by Fermi-function F(E). Let dn represents the number of filled energy states.

In this case of material of absolute zero the upper occupied level is E_F and for all the levels below E_F, F(E)=1 (at T = 0 K the maximum energy level that can be occupied by the electron is called Fermi energy level E_F T = 0 K F(E) = 1).

Integrating equation (8) within the limits 0 to E_F0 us can get the number of energy states of electron (N)

Hence the Fermi energy of a metal depends only on the density of electrons of that metal.

11.2 Average energy of an electron at 0 K

Average energy of electron

12  WORK FUNCTION

It is defined as the minimum energy required to remove an electron from the metal surface at absolute zero (0 K) is called as work function.

12.1 Explanation

Let E_F be the maximum energy of an electron called Fermi energy and E_B be the energy of the metal barrier surface.

          If we supply energy E_B greater than E_F, then no of electron escapes from the metal.

          In order to make it to escape, an additional amount of energy equal to (E_B – E_F ) is required. i.e., E_B + (E_B – E_F )

          This difference in energy E_W = E_B – E_F is called Work function of a metal.

          This Concept is shown in energy diagram.

          Different metals have different work functions.

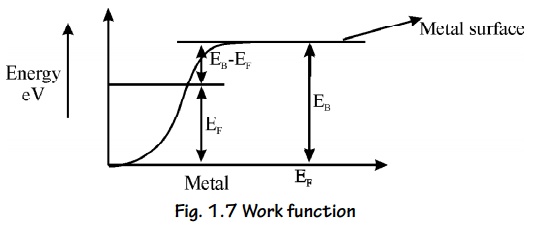
Fig. 1.7 Work function

          Work functions for Some Metals

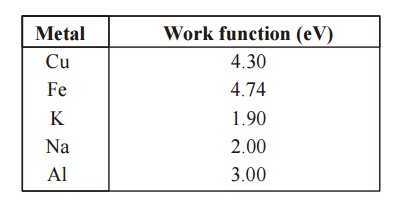
          Metal        : Work function (eV)

          Cu   4.30

          Fe    4.74

          K     1.90

          Na   2.00

          Al    3.00