Area of a Triangle

Area of a Triangle

In your  earlier classes, you have studied how to calculate the area of a triangle when its base and corresponding height (altitude) are given. You have used the formula.

With any three non – collinear points A(x₁ , y₁) , B (x₂ , y₂ ) and C (y₃ , y₃ ) on a plane, we can form a triangle ABC.

Using distance between two points formula, we can calculate AB = c , BC = a , CA = b . a, b, c represent the lengths of the sides of the triangle ABC.

Using 2s = a +b +c , we can calculate the area of triangle ABC by using the Heron’s formula 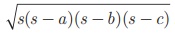. But this procedure of finding length of sides of ΔABC and then calculating its area will be a tedious procedure.

There is an elegant way of finding area of a triangle using the coordinates of its vertices. We shall discuss such a method below.

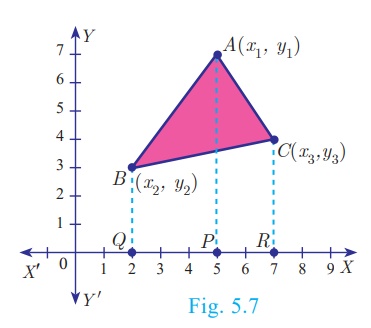
Let ABC be any triangle whose vertices are at A(x₁, y₁ ) , B (x₂, y₂ ) and C (x₃, y₃ ) .

Draw AP, BQ and CR perpendiculars from A, B and C to the x-axis, respectively.

Clearly ABQP, APRC and BQRC are all trapeziums.

Now from Fig.5.7, it is clear that 

Area of ΔABC

= Area of trapezium ABQP + Area of trapezium APRC − Area of trapezium BQRC.

You also know that, the area of trapezium 

= 1/2 ×(sum of parallel sides) ×(perpendicular distance between the parallel sides)

Therefore, Area of ΔABC

= 1/2 (BQ + AP)QP + 1/2 (AP +CR)PR − 1/2 (BQ +CR)QR

= 1/2 (y₂  + y₁ )(x₁ − x₂ ) + 1/2 (y₁ + y₃ )(x₃ − x₁ ) − 1/2 (y₂  + y₃ )(x₃ − x₂ )

= 1/2 {x₁ (y₂ − y₃ ) + x₂(y₃ − y₁ ) + x₃ (y₁ − y₂ )}

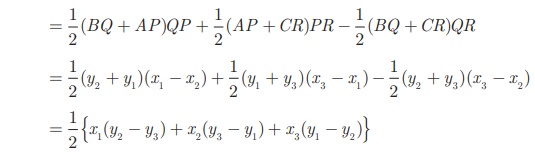
Thus, the area of ΔABC is the absolute value of the expression

= 1/2 {x ₁ (y ₂ − y ₃ ) + x ₂(y ₃ − y₁ ) + x ₃ (y ₁ − y₂ )} sq.units.

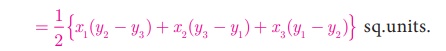
The vertices A(x ₁ , y₁ ) , B (x₂ , y₂ ) and C (x₃ , y₃ ) of ΔABC are said to be “taken in order” if A, B, C are taken in counter-clock wise direction. If we do this, then area of ΔABC will never be negative.

Another form

The following pictorial representation helps us to write the above formula very easily.

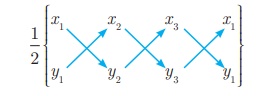
Area of ΔABC = 1/2 {(x ₁ y₂  + x ₂ y₃  + x ₃ y₁ ) −(x ₂ y₁ + x ₃ y₂  + x ₁y₃ )} sq.units.

Note

“As the area of a triangle can never be negative, we must take the absolute value, in case area happens to be negative”.

Progress Check

The vertices of ΔPQR are P(0, - 4) , Q(3, 1) and R(-8, 1)

·           Draw ΔPQR on a graph paper.

·           Check if ΔPQR is equilateral.

·           Find the area of ΔPQR.

·           Find the coordinates of M, the mid-point of QP.

·           Find the coordinates of N, the mid-point of QR.

·           Find the area of ΔMPN.

·           What is the ratio between the areas of ΔMPN and ΔPQR ?

Collinearity of three points

If three distinct points A(x ₁ , y₁ ) , B(x ₂ , y₂ ) and C(x ₃ , y₃ ) are collinear, then we cannot form a triangle, because for such a triangle there will be no altitude (height). Therefore, three points A(x ₁ , y₁ ) , B(x ₂ , y₂ ) and C(x ₃ , y₃ ) will be collinear if the area of ΔABC =0.

Similarly, if the area of ΔABC is zero, then the three points lie on the same straight  line. Thus, three distinct points A(x₁,y₁), B(x₂,y₂) and C(x₃,y₃) will be collinear if and only if area of ∆ABC = 0.