Area of a Quadrilateral

Area of a Quadrilateral

If ABCD is a quadrilateral, then considering the diagonal AC, we can split the quadrilateral ABCD into two triangles ABC and ACD.

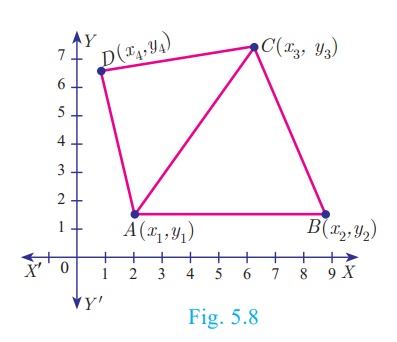
Using area of triangle formula given its vertices, we can calculate the areas of triangles ABC and ACD.

Now, Area of the quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD

We use this information to find area of a quadrilateral when its vertices are given.

Let A(x₁,y₁), B(x₂,y₂), C(x₃,y₃) and D(x₄,y₄) be the vertices of a quadrilateral ABCD.

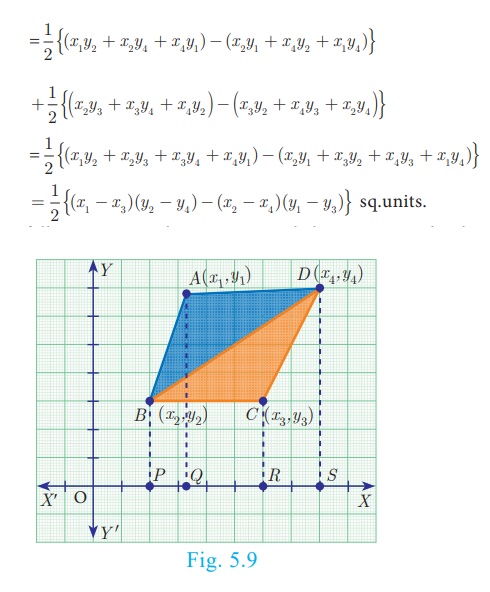
Now, Area of quadrilateral ABCD = Area of the ΔABD + Area of the ΔBCD (Fig5.9)

Thinking Corner : How many triangles exist, whose area is zero?

The following pictorial representation helps us to write the above formula very easily.

Take the vertices A(x₁,y₁), B(x₂,y₂), C(x₃,y₃) and D(x₄,y₄)  in counter-clockwise direction and write them column-wise as that of the area of a triangle.

Therefore, area of the quadrilateral ABCD

= 1/2 {(x ₁y₂ + x ₂y₃ + x ₃y₄  + x ₄y₁ ) − (x ₂y₁ + x₃y₂ + x₄y₃ + x₁y₄ )} sq.units.

Note

·           To find the area of a quadrilateral, we divide it into triangular regions, which have no common area and then add the area of these regions.

·           The area of the quadrilateral is never negative. That is, we always take the area of quadrilateral as positive.

Thinking Corner: If the area of a quadrilateral formed by the points (a, a), (–a, a), (a, –a) and (–a, –a), where a ≠ 0 is 64 square units, then identify the type of the quadrilateral Find all possible values of a.