Angular momentum of a rigid body

Angular momentum of a particle

The angular momentum in a rotational motion is similar to the linear momentum in translatory motion. The linear momentum of a

particle moving along a straight line is the product of its mass and linear velocity (i.e) Vec p = m. Vec v. The angular momentum of a particle is

defined as the moment of linear momentum of the particle.

Let us consider a particle of mass m moving in the XY plane with a velocity v and linear momentum p =   mv  at a distance r from the origin (Fig. ).

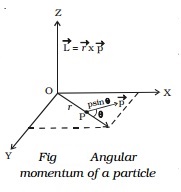
The angular momentum L of the particle about an axis passing through O perpendicular to XY plane is defined as the cross product of Vec  r and Vec  p.

 (i.e) Vec  L = Vec  r ? Vec  P

Its magnitude is given by L = r p sin θ

Where θ is the angle between  Vec r and Vec  p and L is along a direction perpendicular to the plane containing  Vec  r and Vec  p .

The unit of angular momentum is kg m² s^?1 and its dimensional formula is, M L² T^?1.

Angular momentum of a rigid body

Let us consider a system of n particles of masses m₁, m₂ ?.. m_n situated at distances r₁, r₂, ?..r_n respectively from the axis of rotation (Fig. ). Let v₁,v₂, v ₃ ?.. be the linear velocities of the particles respectively, then linear momentum of first particle = m₁v₁.

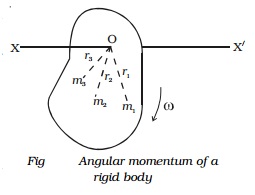
Since v₁= r₁ω the linear momentum of first particle = m₁(r₁ ω)

The moment of linear momentum of first particle

= linear momentum ? perpendicular distance

= (m₁r₁ω) ? r₁

angular momentum of first particle = m₁r₁²ω

Similarly,

angular momentum of second particle = m₂r₂²ω

angular momentum of third particle = m₃r₃²ω and so on.

The sum of the moment of the linear momenta of all the particles of a rotating rigid body taken together about the axis of rotation is known as angular momentum of the rigid body.

 Angular momentum of the rotating rigid body = sum of the angular momenta of all the particles.

(i.e)  L = m ₁r₁ ²ω+ m₂ r₂ ²ω + m₃ r₃²ω.?. + m_n r_n ² ω

L = ω [  m ₁r₁ ²+ m₂ r₂ ²ω + m₃ r₃².?. + m_n r_n ² ]

∴ L = ωI

where I = ∑ m_i r_i ² moment of inertia of the rotating rigid body about the axis of rotation.