Addition Theorem of Probability

Addition Theorem of Probability

(i) If A and B are any two events then

P (A ∪ B ) = P(A) + P(B ) −P(A ∩ B)

(ii) If A,B and C are any three events then

P (A ∪ B ∪ C) = P (A) + P (B) + P (C) − P (A ∩ B ) − P(B ∩C) −P (A ∩C ) + P(A ∩ B ∩C)

Proof

(i) Let A and B be any two events of a random experiment with sample space S.

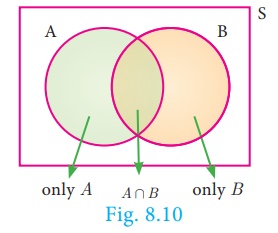
From the Venn diagram, we have the events only A, A Ո B and only B are mutually exclusive and their union is A U B

Therefore, P (A U B)  = P[ (only A) ∪(A ∩ B) ∪ (only B) ]

= P(only A) +P (A ∩ B) + P(only B)

= [P (A) −P (A ∩ B )] + P(A ∩ B) +[P (B ) − P (A ∩ B)]

P (A U B)  = P (A) + P (B ) − P (A ∩ B)

(ii) Let A, B, C are any three events of a random experiment with sample space S.

Let D = B ∪C

P (A U B UC) = P (A ∪ D)

= P (A) + P (D ) − P (A ∩ D)

= P (A) + P (B ∪ C ) − P[A ∩ (B ∪C)]

= P (A) + P (B) + P(C ) − P(B ∩C) − P [(A ∩ B ) ∪ (A ∩C)]

= P (A) + P (B) + P (C) − P (B ∩C ) − P(A ∩ B) − P (A ∩C ) + P[(A ∩ B) ∩ (A ∩C)]

P (A U B UC) = P (A) + P (B) + P (C) − P (A ∩ B ) − P(B ∩C) −P (C ∩ A) + P(A ∩ B ∩C)

Example 8.27

If P(A) = 0.37 , P(B) = 0.42 , P (A ∩ B) = 0.09 then find P (A U B) .

Solution

P(A) = 0.37 , P(B) = 0.42 , P (A ∩ B) = 0.09

P (A U B)  = P (A) + P (B ) − P (A ∩ B)

P (A U B)  = 0.37 + 0.42 − 0.09 = 0. 7

Example 8.28 

What is the probability of drawing either a king or a queen in a single draw from a well shuffled pack of 52 cards?

Solution

Total number of cards = 52

Number of king cards = 4

Probability of drawing a king card = 4/52

Number of queen cards = 4

Probability of drawing a queen card= 4/52

Both the events of drawing a king and a queen are mutually exclusive 

⇒ P (A ∪ B)  = P (A) + P (B)

Therefore, probability of drawing either a king or a queen = 4/52 + 4/52 = 2/13

Example 8.29 

Two dice are rolled together. Find the probability of getting a doublet or sum of faces as 4.

Solution 

When two dice are rolled together, there will be 6×6 = 36 outcomes. Let S be the sample space. Then n (S) = 36

Let A be the event of getting a doublet and B be the event of getting face sum 4.

Then A = {(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}

B = {(1,3),(2,2),(3,1)}

Therefore,  A Ո B = {(2,2)}

Then, n (A) = 6 , n (B) = 3 , n (A ∩ B) = 1.

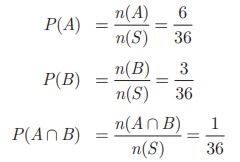
Therefore, P (getting a doublet or a total of 4) = P (A U B)

P (A U B)  = P (A) + P (B ) − P (A ∩ B)

= 6/36 + 3/36 – 1/36 = 8/36 = 2/9

Hence, the required probability is 2/9.

Example 8.30

If A and B are two events such thatP (A) = 1/4 , P (B) = 1/2 and P(A and B)= 1/8, find (i) P (A or B) (ii) P(not A and not B).

Solution

(i) P (A or B)  = P (A U B)

= P (A) + P (B ) − P (A ∩ B)

P (A or B) = 1/4 + 1/2 – 1/8  = 5/8

(ii) P (not A and not B) = P ( ∩ )

= P 

= 1 − P (A ∪ B)

P(not A and not B) = 1 – 5/8 = 3/8

Example 8.31 

A card is drawn from a pack of 52 cards. Find the probability of getting a king or a heart or a red card.

Solution

Total number of cards = 52; n(S) = 52

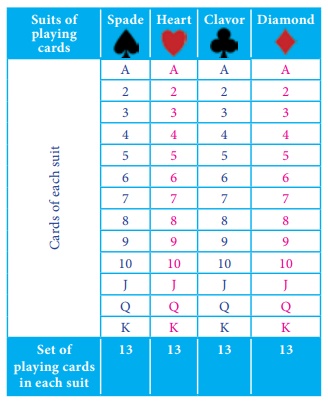
Let A be the event of getting a king card. n(A)  =4

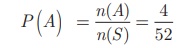
Let B be the event of getting a heart card. n(B) =13

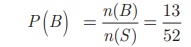
Let C be the event of getting a red card. n(C)  =26

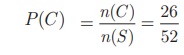
P (A Ո B) = P (getting heart king) = 1/52

P (B ՈC) = P (getting red and heart)) = 13/52

P (A ՈC) = P (getting red king) = 2/52

P (A Ո B ՈC) = P (getting heart, king which is red) = 1/52

Therefore, required probability is

P (A U B UC) = P (A) + P (B) + P (C) − P (A ∩ B ) − P(B ∩C) −P (C ∩ A) + P(A ∩ B ∩C)

 = 4/52 + 13/52 + 26/52 – 1/52 – 13/52 – 2/52 + 1/52 = 28/52 

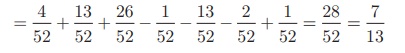
= 7/13

Example 8.32 

In a class of 50 students, 28 opted for NCC, 30 opted for NSS and 18 opted both NCC and NSS. One of the students is selected at random. Find the probability that 

(i) The student opted for NCC but not NSS.

(ii) The student opted for NSS but not NCC.

(iii) The student opted for exactly one of them.

Solution

Total number of students n (S) = 50 .

Let A and B be the events of students opted for NCC and NSS respectively.

n (A) = 28 , n (B) = 30 , n (A ∩ B) = 18

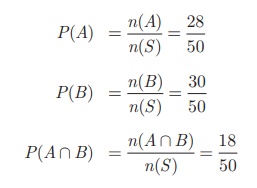
(i) Probability of the students opted for NCC but not NSS

P (A Ո )  = P (A) −P (A ∩ B) = 28/50 – 18/50 =1/5

(ii) Probability of the students opted for NSS but not NCC.

P (A Ո ) = P (B ) −P (A ∩ B) = 30/50 – 18/50 = 6/25

(iii) Probability of the students opted for exactly one of them

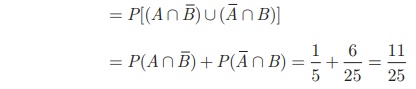
(Note that (A Ո ), (Ո B) are mutually exclusive events)

Example 8.33 

A and B are two candidates seeking admission to IIT. The probability that A getting selected is 0.5 and the probability that both A and B getting selected is 0.3. Prove that the probability of B being selected is atmost 0.8.

Solution 

P (A) = 0.5 , P (A ∩ B) = 0.3

We have P (A U B ) ≤ 1

P (A) + P(B) −P (A ∩ B) ≤ 1

0.5 + P (B) − 0.3 ≤ 1

P (B) ≤ 1 − 0.2

P (B)   ≤ 0.8

Therefore, probability of B getting selected is atmost 0.8.